Априорная и апостериорная оценка качества прогноза
Оценка качества эксперта может быть:
1) априорной – если в ней не используется информация о его участии в других экспертизах (т.е. эксперт оценивается априорно, до того, как он был использован в качестве эксперта) ;
2) апостериорной – если она использует такую информацию (основана на ней) и
3) тестовой – в форме специального тестового испытания, направленного на выявление необходимых качеств эксперта.
К априорным методам оценки относятся:
1) самооценка эксперта. Она может осуществляться
а) с использованием балльной шкалы (например, 5-балльной) ;
б) с использованием других шкал. Например, если необходимо отнести себя к одной из двух групп - «теоретик» или «практик», - то речь идет о самооценке в номинальной шкале (шкале наименований), на которой задано только отношение тождества (либо объект относится к некоторой группе, либо нет). Если необходимо отнести себя к одной из групп: «начинающий исследователь», «исследователь, имеющий опыт работы в данной области», «исследователь с большим опытом работы», «углубленный специалист по исследованиям в данной области», - то речь идет об ординальной шкале (шкале порядков), на которой задано отношение «больше-меньше» («лучше-хуже»). Она может быть дополнена указанием некоторых числовых диапазонов, например, если специалист занимается данной областью исследований менее полугода, его считают начинающим, от полугода до 2 лет – имеющим опыт, от 2 до 5 лет – большой опыт, более 5 – углубленно знакомым с предметом. Более подробно типы шкал будут рассмотрены далее ;
в) путем расчета интегральных (агрегированных) показателей самооценки по различным показателям (например, по уровню знакомства с различными источниками информации в определенной области специалист оценивает себя 5 баллами, а по уровню знакомства с исследуемой проблемой – 4-мя баллами по 5-балльной шкале; если веса этих показателей равны соответственно 0.8 и 0.2, то агрегированная оценка составит 5*0.8 + 4*0.2 = 4.8). Подробнее способ расчета агрегированных показателей был рассмотрен при изучении принципа оптимальности;
Недостатком всех методов самооценки является то, что такая оценка тесно связана с уровнем самокритичности, что затрудняет ее интерпретацию. Достоинством является простота получения такой оценки.
2) взаимная оценка экспертов. Здесь, в свою очередь, потенциальным членам экспертной группы могут быть предложены различные методы оценки друг друга – балльные оценки, сравнительные оценки, простое формирование списков и т.п. (подробнее рассматривается далее). Полученные от разных экспертов оценки подлежат дальнейшей обработке для получения отдельной оценки для каждого эксперта. Т.е. такая оценка, в свою очередь, является групповой экспертной оценкой, и встает проблема ее обработки для получения общей оценки (см. далее). Такая оценка предположительно является более объективной, чем самооценка, но
Процесс ее получения более сложен;
- кроме того, здесь также могут проявиться личностные и групповые симпатии и антипатии, что повлияет на объективность;
- и, наконец, различные эксперты по одному и тому же вопросу не обязательно хорошо знакомы с работами и возможностями друг друга. В современных условиях такое знакомство может быть лишь у специалистов, длительно работающих совместно. Однако их одновременное привлечение к экспертизе может быть не целесообразно, поскольку они слишком похожи друг на друга.
3) документационный метод (так называемый метод объективных оценок, или метод формальных показателей) – основан на использовании соответствующим образом заверенных документов, содержащих объективную информацию об эксперте (диплом, трудовая книжка и т.п.). Например, для вхождения в экспертную группу могут быть предъявлены следующие требования: стаж работы не менее трех лет (подтверждается выпиской из трудовой книжки), высшее образование (подтверждается дипломом), не менее 10 научных трудов (подтверждается списком, заверенным соответствующим лицом). Объективность оценки, полученной по данному методу, зависит от добросовестности и объективности суждений лиц, выдающих и заверяющих используемые документы, а также репутации соответствующих организаций (например, дипломы разных вузов объективно имеют различную ценность, стаж работы в различных организациях также неравноценен и т.п.). Рекомендуется использовать данный метод только как вспомогательный.
4) и прочие методы.
Исследуем теперь точность оценок максимального правдоподобия и байесовских оценок в условиях, когда априорные значения математических ожиданий и дисперсий известны неточно. Будут рассмотрены два случая. В первом из них будет предполагаться, что априорная плотность вероятности параметра неизвестна, хотя значения ее первых двух моментов заданы; при этом также считается известной условная плотность вероятности . Для этого случая можно найти оценку максимального правдоподобия . Но поскольку среднеквадратическая ошибка байесовской оценки меньше, чем оценки максимального правдоподобия (см. пример 6.7), то вполне можно считать оправданными попытки использования псевдобайесовской оценки, при построении которой вместо недостающей априорной плотности вероятности оцениваемого параметра вводится какая-либо другая плотность. При анализе первого случая такой вводимой функцией служит нормальная плотность вероятности. При этом будет показано, что получающаяся псевдобайесовская оценка имеет меньшую среднеквадратическую ошибку, чем оценка максимального правдоподобия. Во втором случае будем считать, что неизвестными являются также и среднее значение, и дисперсия оцениваемого параметра. В подобных условиях будет предложено использовать эмпирические псевдобайесовские оценки, основывающиеся на априорных оценках неизвестных значений математического ожидания и дисперсии.
Анализ точности: оценки максимального правдоподобия. Рассмотрим линейную модель наблюдений:
где и - векторы с компонентами, представляющие собой выборку и вектор шума; - постоянный N-мерный параметр, подлежащий оцениванию; - модуляционная матрица размера .Будем предполагать, что является нормальным случайным вектором с нулевым средним значением и ковариационной матрицей
Оценка максимального правдоподобия для параметра определяется максимизацией по плотности вероятности
 (6.56)
(6.56)
; ;  .
.
Нетрудно доказать, что
В действительности часто оказывается, что ковариационные матрицы шума известны лишь приближенно. Поэтому примем, что вместо точных матриц или в алгоритме оценивания используются несколько отличающиеся матрицы или . Так что фактически будет вычисляться оценка
которая является несмещенной при каждом фиксированном значении оцениваемого параметра (условно несмещенной). Рассмотрим теперь следующие ошибки:
; ![]() ;
; ![]() . (6.59)
. (6.59)
Здесь является ошибкой, которая получается при использовании алгоритма для вычисления значений оценки максимального правдоподобия, ориентированного на точную ковариационную матрицу (такую оценку назовем идеальной); - ошибка оценивания, когда используемый алгоритм ориентирован на предполагаемую матрицу ; разность между значениями действительной оценки максимального правдоподобия и вычисляемой обозначена символом .
Из ф-лы (6.25) для безусловной среднеквадратической ошибки получаем
 , (6.60)
, (6.60)
если для оценивания используется идеальная оценка максимального правдоподобия. С другой стороны, для оценки имеем:
или с использованием обозначений, принятых в (6.54),
Можно показать (см. § 6.7), что
Полезно рассмотреть разность двух анализируемых оценок, поскольку она характеризует точность вычисления значений идеальной оценки максимального правдоподобия. Для ковариационной матрицы вектора получаем
Рассмотрим теперь случай, когда предполагаемая ковариационная матрица шума «близка» к истинной, т. е. можно положить
где «мало». Тогда
![]() (6.67)
(6.67)
Используя это приближение и учитывая также, что

получаем
Пример 6.10. В скалярном стационарном случае, когда
приходим к следующим выражениям для оценок и их дисперсий:
 ;
; ![]() ;
;  ;
; ![]() ;
;
Интересным оказывается тот факт, что для этого частного случая не нужно знать дисперсию шума при вычислении оценки максимального правдоподобия. И это справедливо всякий раз, когда выборка является скалярной, а ее элементы независимы и одинаково распределены.
Пример 6.11. Допустим теперь, что предполагаемая ковариационная матрица шума отличается от истинной, причем
Выражения для рассматриваемых оценок и их ковариационных матриц при этом имеют вид
; ![]() ;
;
так что вновь оценка максимального правдоподобия оказывается нечувствительной к подобным ошибкам в определении ковариационной матрицы шума.
Пример 6.7 позволил показать, что оценка максимального правдоподобия хуже, чем байесовская оценка. Она приводит к большей среднеквадратической ошибке оценивания, поскольку при построении оценки максимального правдоподобия совсем не учитывается априорная плотность вероятности оцениваемого параметра. Перейдем теперь к анализу точности байесовских оценок.
Анализ точности: байесовские оценки. Снова рассмотрим линейную модель наблюдаемого процесса
где случайный параметр является -мерным вектором, выборочное значение которого одно и то же для всех элементов выборки; векторы и имеют размерность , а модуляционная матрица наблюдений - размер. Будем предполагать, что и - независимые нормальные векторы с параметрами:
Как и в примере 6.1, для оценки по максимуму апостериорной плотности вероятности получаем
Ковариационная матрица вектора ошибок при использовании этой оценки
Предположим теперь, что вместо истинных математических ожиданий и ковариационных матриц в ф-ле (6.73) используются другие матрицы , и или для составного вектора. Так что фактически вычисляется оценка
которая не является уже безусловно несмещенной, так как
Оценка будет несмещенной только в том случае, когда – либо , либо . Корреляционная матрица вектора ошибок при использовании этой оценки вычисляется обычным образом с использованием (6.74) Так как
 (6.77)
(6.77)
Эта матрица зависит от величины смещения оценки [см. второе слагаемое в ф-ле (6.76)] Ковариационная матрица вектора ошибок для оценки
Если ковариационные матрицы, используемые при вычислении оценки , оказываются равными истинным, то ф-ла (6.79) переходит в (6.74). Во всех же других случаях
и равенство достигается тогда, когда ; . Разница между знаменателями двух
рассматриваемых оценок ![]() получается путем вычитания (6.75) из
(6.73). Ковариационную матрицу этого вектора, можно вычислить с помощью соотношения
получается путем вычитания (6.75) из
(6.73). Ковариационную матрицу этого вектора, можно вычислить с помощью соотношения
Так что окончательно имеем
Эта матрица равна нулю, если моменты, используемые при вычислении оценки , совпадают с истинными. Формулы (6.76) и (6.82) позволяют провести анализ точности оценки по максимуму апостериорной плотности вероятности при неточно известных ковариационных матрицах оцениваемого параметра и шума.
Полезные приближения для полученных выражений можно указать для случая, когда
![]() ; ; , (6.83)
; ; , (6.83)
где и малы. Для этого достаточно воспользоваться следующими приближенными представлениями:
Если ошибки в определении априорных ковариационных матриц малы, то использовать это выражение несколько проще, чем (6.82). Однако более важным следствием, вытекающим из ф-лы (6.84) и касающимся точности оценок и является то, что согласно (6.84) ковариационная матрица вектора разности этих оценок пропорциональна , и . То есть, если при вычислении оценки используются ковариационные матрицы, отличающиеся от истинных на , то это приводит к увеличению на дисперсий ошибок оценивания. Аналогичное замечание следует сделать относительно ф-лы (6.69), определяющей ковариационную матрицу вектора разности двух оценок максимального правдоподобия.
Приведенные выше соотношения позволяют оценить ухудшение точности оценок максимального правдоподобия и байесовских оценок при неправильном выборе априорных средних значений и ковариационных матриц. Показано, что оценка максимального правдоподобия всегда остается несмещенной. Однако байесовская оценка оказывается смещенной, если априорное среднее значение отлично от истинного, либо выбранная обратная ковариационная матрица не равна нулю. Если же принимается равной нулю, то байесовская оценка переходит в оценку максимального правдоподобия.
Исследуем теперь смещение последовательных оценок, возникающее из-за неточного знания априорных данных. Снова примем, что
Однако при построении последовательной оценки для параметра , вычисляемой на каждом шаге , , было принято, что априорное среднее значение ковариационная матрица этого параметра равны соответственно и .
Сначала будем предполагать, что ковариационная матрица шума уже выбрана и может считаться заданной, в то время как и неизвестны и вместо них будут использоваться оценки и .
В соответствии с (6.73) имеем
 , (6.86)
, (6.86)
где - оценка по максимуму апостериорной плотности вероятности (или байесовская оценка при симметричной функции потерь) для параметра , вычисляемая по выборке . При эта оптимальная оценка имеет вид
Если теперь использовать предложенные оценки и вместо и и воспользоваться леммой об обращении матриц, то последнее выражение можно переписать следующим образом:
При получаем
Это выражение можно переписать следующим образом:
где ; ![]() .
.
Здесь снова использована лемма об обращении матриц. Повторяя подобные рассуждения для можно установить следующее рекуррентное соотношение:
 (6.89)
(6.89)
Это и есть искомые алгоритмы последовательного оценивания. Полученные выражения являются частным случаем алгоритмов, описывающих фильтры Калмана и Винера, которые будут обсуждаться в следующей главе. Эти соотношения можно получить также непосредственно из общего выражения для оценки , если учесть, что
 (6.91)
(6.91)
Эти оба набора соотношений можно использовать для построения алгоритма последовательного вычисления оценки. Если размерность векторов или меньше размерности вектора , то набор соотношений (6.89) намного предпочтительнее с вычислительной точки зрения. Это объясняется тем, что в этом случае при вычислении значений оценки требуется обращать матрицы более низкого размера. Очевидно также, что оба набора соотношений приводят к более сложным вычислениям, чем исходное выражение для оценки
 . (6.92)
. (6.92)
Поэтому это выражение и следует использовать при практических вычислениях, если нет необходимости в последовательном получении значений оценок. Если же требуются последовательные алгоритмы, то необходимо использовать соотношения (6.89). Следует, однако, иметь в виду, что подобными рекомендациями можно руководствоваться не всегда. Обычно последовательные алгоритмы более предпочтительны с точки зрения их реализации по сравнению с непоследовательными.
Найдем теперь смещение оценки при использовании последовательного алгоритма. Пусть - истинное среднее значение оцениваемого параметра. Тогда смещение
 . (6.93)
. (6.93)
Отсюда следует, что смещение оценки стремится к нулю при , так что эта оценка асимптотически несмещена. Смещение уменьшается также с ростом априорной ковариационной матрицы . Кроме того,
 (6.94)
(6.94)
так что при достаточно большом числе наблюдений априорное
среднее значение и ковариационная матрица вектора не оказывают существенного
влияния на вычисляемые значения оценок. Однако при малых значениях смещение оценки по
максимуму апостериорной плотности вероятности, обусловленное неточностью
априорных оценок среднего значения и ковариационной матрицы вектора , может быть
существенным. Если выбранная матрица отличается от истинной матрицы шума то ковариационная матрица
фактически вычисляемой оценки может быть найдена по ф-ле (6.78). Так что для
ковариационной матрицы ошибки ![]() получаем
получаем
где и - предполагаемые, a и - истинные ковариационные матрицы. Выражение для смещения было приведено выше. Заметим, что только в том случае, когда предполагаемые матрицы оказываются равными истинным, выражение для ковариационной матрицы совпадает с приведенным ранее выражением для матрицы . В гл. 8 будет показано, что найденное здесь соотношение для ковариационной матрицы ошибок можно записать в форме разностного уравнения. Здесь же приведем выражение для ковариационной матрицы ошибок при использовании оценки после достаточно большого числа шагов. Имеем
При смещение и ковариационная матрица этой оценки стремятся к нулю, даже если ковариационная матрица шума неизвестна. Подчеркнем, однако, что эти выводы остаются справедливыми только для этого частного примера, в котором оцениваемый параметр не меняет своего значения от наблюдения к наблюдению. В общем случае, когда значения оцениваемого параметра изменяются во времени, и смещение оценки, и ковариационная матрица вектора ошибок не стремятся к нулю с ростом времени наблюдения или объема выборки .
Пример 6.12. Если предположить, что и являются скалярными величинами и дисперсия шума не зависит от номера наблюдения, то полученные выше соотношения существенно упрощаются. Действительно, в этом случае совокупность алгоритмов последовательного оценивания (6.89) принимает вид
![]() ; ;
; ;
 ; .
; .
Непоследовательная оценка и предполагаемая дисперсия этой оценки могут быть найдены в результате решения этих разностных уравнений. Так что
 ;
;  .
.
Смещение оценки
 .
.
Дисперсия фактически вычисляемой оценки
 .
.
Согласно (6.82) для дисперсии разности двух оценок получаем
 .
.
Это выражение не удается привести к более простому виду, поэтому может оказаться полезной приближенная формула типа (6.84)
На рис 6.9
приведены графики, иллюстрирующие влияние априорной дисперсии на нормированное
смещение оценки при .
Если намного
больше, чем ,
смещение с ростом объема выборки быстро уменьшается. Поэтому если в
практических задачах смещение оценки при малых нежелательно, то значение не следует брать
слишком малым. Конечно, если истинное значение априорного среднего известно и
используется при вычислении оценки, то смещение отсутствует. На рис 6.10
приведены графики зависимости среднеквадратической ошибки оценивания для двух
случаев. В первом из них , во втором случае исследовалась
зависимость среднеквадратической ошибки при ![]() , причем принятое значение дисперсии шума
не совпадало с истинным.
, причем принятое значение дисперсии шума
не совпадало с истинным.

Рис 6.9 Нормированное смещение оценки как функция объема выборки (пример 6.12)
Второй график
рис. 6.10 справедлив также для случая, когда ![]() , однако значение априорной дисперсии
, однако значение априорной дисперсии
параметра выбрано неверно. Во всех случаях предполагалось, что . Соотношения, необходимые для построения графиков, получены с использованием приближенного представления (6.84) Для рассматриваемых здесь случаев получаем
 ;
;  .
.

Рис 6.10 Дисперсии ошибок оценивания как функции от объема выборки (пример 6.12)
Разность между значениями среднеквадратической ошибки оценивания при использовании указанных алгоритмов и минимально достижимой ошибки оказывается максимальной при объеме выборки и уменьшается с ростом . Если неизвестными являются обе дисперсии и , то тот же приближенный способ вычисления приводит к выражениям
 ;
;  .
.
Теперь разность между значениями среднеквадратических ошибок оказывается наибольшей при объеме выборки, совпадающем с ближайшим целым числом, превышающим . Если то максимум этой разности всегда достигается при .
Аналогичные результаты можно получить для процессов с непрерывным временем. Для наблюдаемого процесса в этом случае можно записать
![]() , (6.97)
, (6.97)
где вектор и шум независимы и являются нормальными, с параметрами:
Соответствующая запись для дискретного времени, которая уже
была использована выше, имеет вид (6.85), где теперь необходимо положить ![]() . Вновь предположим,
что при определении алгоритмов оценивания неизвестная априорная дисперсия
шума принята равной
. Вновь предположим,
что при определении алгоритмов оценивания неизвестная априорная дисперсия
шума принята равной ![]() .Будем считать также, что возможны ошибки
при выборе значений и
. Воспользовавшись
уже известным предельным переходом, из (6.89) получаем следующие
последовательные алгоритмы фильтрации при непрерывном времени:
.Будем считать также, что возможны ошибки
при выборе значений и
. Воспользовавшись
уже известным предельным переходом, из (6.89) получаем следующие
последовательные алгоритмы фильтрации при непрерывном времени:
 (6.98)
(6.98)
Явное выражение для оценки имеет вид
Смещение этой оценки
 , (6.100)
, (6.100)
а матрица вектора ошибок
 (6.101)
(6.101)
Теперь нетрудно выписать аналогичные выражения для только что рассмотренного скалярного случая при непрерывном времени. Необходимые для этого рассуждения полезно провести читателю самостоятельно.
До сих пор при анализе ошибок оценивания не предпринимались попытки уточнить значение дисперсии шума. Теперь попытаемся это сделать. Будем рассматривать последовательность наблюдаемых случайных величин
где случайные величины независимы, нормальны, имеют нулевое среднее значение и одну и ту же дисперсию . Будем исследовать байесовскую оценку для параметра , который является нормальным случайным вектором с известными моментами ; . В соответствии с (6.73) байесовская оценка
Отсюда ясно, что для того, чтобы воспользоваться этим выражением для вычисления значений оценки необходимо знать дисперсию шума. Поскольку для построения байесовской оценки дисперсии шума потребовалось бы вводить плотность вероятности этой дисперсии, то здесь в качестве оценки для ковариационной матрицы используем оценку максимального правдоподобия. Такой выбор будет более обоснованным, если относительно параметра , предположить, что он неслучаен и его значение неизвестно, а не считать его случайным. Подобные логические рассуждения приводят к выбору из двух возможных оценок оценки максимального правдоподобия. В примере 6.6 уже было показано, что в рассматривающихся здесь условиях оценки максимального правдоподобия для параметров и имеют вид
 (6.104)
(6.104)
Сразу же становится очевидным, что при попытке решать эту систему уравнений относительно оценок для параметров или неизбежно возникнут значительные трудности. Их можно обойти, если задачу оценивания сформулировать несколько иначе. А именно, от -мерных векторных наблюдений , перейдем к скалярным наблюдениям , .
Если предположить, что ![]() , то рассматриваемые оценки
максимального правдоподобия примут вид
, то рассматриваемые оценки
максимального правдоподобия примут вид
 ; (6.105)
; (6.105)
 . (6.106)
. (6.106)
Теперь для вычисления значений оценки не нужно знать значение оценки . В то же время значения оценки используются при вычислении оценки .
Если необходимо указать последовательные алгоритмы оценивания,
то можно воспользоваться подходом, который уже был приманен ранее для получения
последовательных оценок . Введем сначала обозначение  . Заметим, что
. Заметим, что
Используя лемму об обращении матриц, получим
Для оценки максимального правдоподобия вектора состояния можно записать
 ;
;  .
.
Объединяя эти два равенства, получаем
Снова используя лемму об обращении матриц применительно к матрице , имеем окончательно
Аналогичным образом можно найти последовательный алгоритм для оценки . В результате получаем
Эти последние два алгоритма могут быть использованы для последовательного адаптивного оценивания. Алгоритмы для более сложных случаев можно найти в работах .
Псевдобайесовские оценки. Покажем, что при оценивании случайного параметра среднеквадратическая ошибка оценивания при использовании оценки максимального правдоподобия больше, чем при использовании байесовской оценки. Именно это имея в виду, будем говорить, что оценка максимального правдоподобия хуже байесовской. Основная причина такого соотношения оценок состоит в том, что при построении байесовской оценки учитываются некоторые априорные сведения об оцениваемом параметре, в то время как при отыскании оценок максимального правдоподобия подобные сведения игнорируются. Правда, к сожалению, неправильный выбор значений параметров априорных распределений приводит к появлению смещения байесовской оценки. Вычисление смещения в таких условиях может оказаться трудно разрешимой проблемой. Таким образом, желательно использовать байесовские оценки с тем, чтобы обеспечить минимально возможное значение среднеквадратической ошибки. Однако при этом необходимо предусмотреть подстройку значений параметров априорного распределения с целью уменьшения смещения оценки.
Рассмотрим линейную модель при дискретном времени, когда
а и независимы и
 (6.110)
(6.110)
Ранее уже было найдено выражение для оценки максимального правдоподобия для этого случая при дополнительном предположении, что шум является нормальным. Чтобы найти оценку максимального правдоподобия, основывающуюся на одном единственном наблюдении, необходимо максимизировать значение плотности . Это приводит к следующему выражению:
Условные математическое ожидание и ковариационная матрица этой оценки равны соответственно:
 (6.112)
(6.112)
Таким образом, эта оценка является несмещенной, а ее ковариационная матрица
и совпадает с условной ковариационной матрицей.
Чтобы найти оценку максимального правдоподобия, основывающуюся на выборке объема , необходимо максимизировать значение плотности вероятности , где - выборка объема . В соответствии с (6.57) имеем
 . (6.114)
. (6.114)
Эта оценка не смещена, так как
![]() , (6.115)
, (6.115)
а ее ковариационная матрица
 . (6.116)
. (6.116)
Ранее было получено также выражение для оценки по максимуму апостериорной плотности вероятности для случая, когда параметр являлся нормальной случайной величиной. Если оценка должна основываться на одном наблюдении , то ее значения отыскиваются путем максимизации апостериорной плотности вероятности . В соответствии с (6.73) имеем
Эта оценка является несмещенной, так как ![]() . Согласно (6.74) ее
ковариационная матрица
. Согласно (6.74) ее
ковариационная матрица
Если же оценка по максимуму апостериорной плотности вероятности должна основываться на выборке объема , то для ее отыскания необходимо максимизировать значение апостериорной плотности вектора при условии, что значение выборки фиксировано. Эта процедура максимизации приводит к следующему выражению для оценки:
Можно также показать, что
 . (6.120)
. (6.120)
Сравнивая матрицы (6.116) и (6.120), нетрудно заметить, что можно записать в виде
 . (6.121)
. (6.121)
Используя теперь лемму об обращении матриц, получаем
Заметим, что вторая матрица в правой части этого равенства неотрицательно определена. Это означает, что среднеквадратическая ошибка оценивания при использовании оценки по максимуму апостериорной плотности вероятности всегда меньше или, в крайнем случае, равна ошибке оценивания при применении оценки максимального правдоподобия.
Если среднее значение и ковариационная матрица параметра известны, но функциональный вид плотности вероятности этого параметра неизвестен, то оценку по максимуму апостериорной плотности вероятности найти нельзя. Поскольку оценка при нормальных оцениваемом параметре и шуме зависит только от среднего значения и ковариационных матриц этого параметра и шума, то можно попытаться использовать оценку в указанных выше условиях даже при неизвестной плотности вероятности параметра . Эту оценку будем называть псевдобайесовской. Как будет показано в следующем разделе, подобная псевдобайесовская оценка эквивалентна линейной оценке с минимальной среднеквадратической ошибкой.
Среднеквадратические ошибки оценивания при использовании псевдобайесовской оценки и оценки по максимуму апостериорной плотности вероятности одинаковы. Это следует из того, что алгоритмы этих оценок одинаковы, а три вычислении соответствующих им среднеквадратических ошибок используются только моменты второго порядка. Если распределения оцениваемого параметра и шума являются нормальными, то наилучшей будет оценка по максимуму апостериорной плотности вероятности. Если же распределение вектора отлично от нормального, то наилучшей линейной оценкой оказывается псавдобайесовская оценка. В этом случае, вообще говоря, могут существовать нелинейные алгоритмы оценивания, обеспечивающие меньшую среднеквадратическую ошибку.
Предположим теперь, что среднее значение и ковариационная матрица априорного распределения неизвестны. Можно найти оценки этих параметров, основывающиеся на выборке объема , и использовать эти оценки при построении псевдобайесовской оценки для параметра . Оценки параметров априорного распределения обозначим соответственно и . Если эти оценки используются при построении псевдобайесовской оценки, то ее будем называть эмпирической псевдобайесовской оценкой. Условия оценивания при этом оказываются точно такими же, как и при построении оценки (6.75), т. е. для эмпирической псевдобайесовской оценки, основывающейся на выборке объема , можно записать
Соответствующая корреляционная матрица вектора ошибок определяется тем же выражением, что и матрица (6.79), т. е.
 (6.124)
(6.124)
Построенная таким образом псевдобайесовская оценка смещена. Ее смещение можно найти с помощью соотношения (6.76). Так что
Можно показать, что если оценки и являются выборочным средним и выборочной ковариационной матрицей соответственно и вычисляются по результатам априорных наблюдений, то эмпирическая псевдобайесовская оценка параметра асимптотически не смещена. Это является следствием несмещенности выборочного среднего .
Если среднее значение и ковариационная матрица параметра неизвестны, то в качестве оценок и будем использовать оценки максимального правдоподобия. К сожалению, в том случае, когда априорная плотность вероятности вектора не является нормальной, выборочное среднее и выборочная ковариационная матрица априорных оценок параметра не являются статистически независимыми оценками. Наличие статистической зависимости между этими оценками существенно усложняет вычисление корреляционной матрицы вектора ошибок при использовании эмпирической псевдобайесовской оценки. Поэтому здесь будем предполагать, что случайные векторы и являются нормальными.
Предположим далее, что можно осуществить наблюдений. Пусть в течение каждого наблюдения записывается выборка объемом . Будем считать также, что значение параметра случайным образом и независимо изменяется от наблюдения к наблюдению. Вычислим значений оценки максимального правдоподобия
 , , (6.126)
, , (6.126)
где - оценка значения параметра при -м наблюдении, основывающаяся на выборке
объема . Очевидно, что
;  . (6.127)
. (6.127)
Таким образом, при конечном объеме выборки оценка сама является
нормальной случайной величиной. Так как для любых двух оценок и ![]() , то эти оценки статистически
независимы. Напомним здесь, что если взаимная ковариационная матрица двух
нормальных случайных векторов равна нулю, то эти векторы независимы., запишем имеет вид и фактически является
отношением мощности сигнала к общей мощности принятого колебания. Таким
образом, если объем выборки больше десяти, то эмпирическая
псевдобайесовская оценка намного лучше, чем оценка максимального правдоподобия,
если критерием сравнения является величина среднеквадратической ошибки
оценивания. Причем выигрыш в точности увеличивается с уменьшением значения параметра
. Другими
словами, при малых отношениях сигнал/шум эмпирические псевдобайесовские оценки
могут обеспечить значительно более высокую точность оценивания по сравнению с оценками
максимального правдоподобия (или с байесовскими оценками при неправильно установленных
значениях параметров априорных распределени, когда нет возможности оценить
эти параметры). Если объем выборки неограниченно возрастает, то
эмпирическая псевдобайесовская оценка почти эквивалентна байесовской оценке,
использующей точные значения параметров априорного распределения вектора . Это объясняется тем,
что при больших объемах выборки значения оценок максимального правдоподобия
мало отклоняются от истинных значений оцениваемых параметров. При больших
объемах выборки неограниченно
увеличивается, то можно доказать, что являются
истинными значениями параметров априорного распределения величины к
дисперсии ошибки оценивания. Для приемника максимального правдоподобия
дисперсия ошибки оценивания определяется выражением (6.106). Поэтому для
отношения сигнал/шум (на
, то эти оценки статистически
независимы. Напомним здесь, что если взаимная ковариационная матрица двух
нормальных случайных векторов равна нулю, то эти векторы независимы., запишем имеет вид и фактически является
отношением мощности сигнала к общей мощности принятого колебания. Таким
образом, если объем выборки больше десяти, то эмпирическая
псевдобайесовская оценка намного лучше, чем оценка максимального правдоподобия,
если критерием сравнения является величина среднеквадратической ошибки
оценивания. Причем выигрыш в точности увеличивается с уменьшением значения параметра
. Другими
словами, при малых отношениях сигнал/шум эмпирические псевдобайесовские оценки
могут обеспечить значительно более высокую точность оценивания по сравнению с оценками
максимального правдоподобия (или с байесовскими оценками при неправильно установленных
значениях параметров априорных распределени, когда нет возможности оценить
эти параметры). Если объем выборки неограниченно возрастает, то
эмпирическая псевдобайесовская оценка почти эквивалентна байесовской оценке,
использующей точные значения параметров априорного распределения вектора . Это объясняется тем,
что при больших объемах выборки значения оценок максимального правдоподобия
мало отклоняются от истинных значений оцениваемых параметров. При больших
объемах выборки неограниченно
увеличивается, то можно доказать, что являются
истинными значениями параметров априорного распределения величины к
дисперсии ошибки оценивания. Для приемника максимального правдоподобия
дисперсия ошибки оценивания определяется выражением (6.106). Поэтому для
отношения сигнал/шум (на
Здесь определяется ф-лой (6.136). Можно
воспользоваться соотношением (6.134) и выписать выражение для отношения
сигнал/шум на выходе приемника, реализующего эмпирическую псевдобайесовскую оценку ![]() .
Коэффициент определяется
ф-лой (6.135). При больших объемах выборки можно получить приближенное
аналитическое выражение, характеризующее выигрыш в точности оценивания при
применении псевдобайесовской оценки по сравнению с оценкой максимального
правдоподобия. Для этого достаточно воспользоваться приближенным соотношением
(6.137).
.
Коэффициент определяется
ф-лой (6.135). При больших объемах выборки можно получить приближенное
аналитическое выражение, характеризующее выигрыш в точности оценивания при
применении псевдобайесовской оценки по сравнению с оценкой максимального
правдоподобия. Для этого достаточно воспользоваться приближенным соотношением
(6.137).
Для рассмотренного здесь примера значение отношения сигнал/шум на выходе байесовского приемника превышает отношение сигнал/шум на выходе приемника максимального правдоподобия ровно в раз, причем обозначение и графиков для приведенных на рис. 6.10.
Апостериори – на основании опыта.
Априори – независимо от предшествующего опыта.
Оценка качества прогноза – одна из центральных проблем в процессе разработки управленческих решений. Степень доверия к разработанному прогнозу во многом влияет на принимаемое решение и сказывается на эффективности управленческих решений, принимаемых с использованием разработанного прогноза.
Однако, как это ни кажется неожиданным, оценка качества прогноза является достаточно сложной задачей не только в момент, когда прогноз только разработан (априорная оценка), но и в момент, когда прогнозируемое событие уже произошло (апостериорная оценка). Прежде чем приступить к обсуждению оценки качества прогноза, отметим тот важный для более четкого понимания процесса принятия решения факт, что качественный прогноз при принятии решения может быть использован по-разному. Если со стороны руководства организации не оказывается значительное воздействие на ход развития событий, а лишь осуществляется наблюдение за ним, то после окончания прогнозируемого периода не-обходимо лишь сопоставить значения спрогнозированных показателей и параметров с полученными в действительности. Это позволяет оценить качество разработанного прогноза апостериорно.
В то же время, пожалуй, более действенным может оказаться использование результатов разработанного прогноза в случае, когда ЛПР может оказать влияние на ход развития событий. Примером такого влияния может являться, в частности, корректировка управляющих воздействий на основании ожидаемых спрогнозированных значений показателей и параметров. Это так называемый активный прогноз. Однако если в результате анализа спрогнозированных значений показателей и параметров ЛПР изменил управляющие воздействия, которые, в свою очередь, изменили развитие прогнозируемых событий, причем нередко в сторону более благоприятную для ЛПР, то вряд ли корректно первоначально разработанный прогноз считать неточным.
Если бы прогноз не был разработан, то не было бы принято и последовавшее за его разработкой эффективное управленческое решение.
После того как прогноз разработан, должны быть определены критерии, по которым точность прогноза может быть оценена.
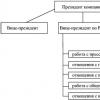
Как правило, для оценки прогноза используются два метода: дифференциальный или интегральный.
При дифференциальном методе оцениваются наборы оценок отдельных составляющих качества прогноза, имеющих достаточно четкий объективный смысл.
В частности, могут использоваться такие критерии, как ясность и четкость задания на прогноз, соответствие прогноза заданию, своевременность разработки прогноза, профессиональный уровень разработки прогноза, надежность использованной информации и т. д.
Интегральный метод предполагает обобщенную оценку качества прогноза на базе оценки качества прогноза по частным критериям.
Однако в ряде случаев этот способ оказывается недостаточно убедительным, поскольку к оценке качества прогноза по частным критериям вольно или невольно добавляется необходимость оценки сравнительной важности критериев и их влияния на интегральную оценку.
Примером использования интегрального метода может служить критерий «интегрального качества экспертного прогноза» – оценка прогноза, по которому предполагает, в частности, и оценку по перечисленным выше частным критериям.
Если говорить об экспертном прогнозе, то его качество определяется, прежде всего, такими частными критериями, как:
– компетентность (или в более общем виде – качество) эксперта;
– качество информации, предоставляемой экспертам;
– качество экспертной информации, поступающей от экспертов;
– уровень технологии разработки прогноза или, иными словами, качество методов и процедур, используемых при разработке прогноза.
Если период прогнозирования уже завершился, то необходимо сопоставить спрогнозированные значения показателей и параметров с полученными в результате реализовавшегося с действительности хода прогнозируемых событий.
Для проведения такой оценки необходимо принять во внимание все основные факторы, определяющие качество разработанного прогноза.
7. Контроль хода реализации и корректировки прогноза . После того как прогноз подготовлен и представлен руководству организации, заказчику и т. д., наступает новый этап работы с подготовленным материалом.
Вариантная разработка прогноза также предполагает разработку прогноза при различных альтернативных вариантах условий и предположений, которые могут изменяться. События, вчера казавшиеся маловероятными, сегодня происходят, а казавшиеся наиболее вероятными не происходят вовсе. Базируясь на устаревшем, не учитывающем реалии действительного развития событий прогнозе, трудно принять эффективное управленческое решение.
Поэтому неотъемлемой частью современной технологии прогнозирования является периодически осуществляемый (в зависимости от происходящих изменений) мониторинг хода реализации прогнозированного развития событий.
Мониторинг позволяет своевременно выявлять значительные отклонения в ходе развития событий.
Если они могут оказать принципиальное влияние на дальнейший ход событий в части, касающейся принятия важных стратегических решений, то прогноз должен быть подвергнут корректировке.
Необходимо отчетливо понимать, что прогнозы ценны не сами по себе, как возможность профессионального предсказания ожидаемого хода развития событий в той или иной области человеческой деятельности, а в большей степени как необходимый и очень существенный элемент разработки важных управленческих решений.
Поэтому при выявившихся значительных отклонениях в ходе развития событий в прогнозируемой области деятельности, особенно в случае активного прогноза, в уже разработанный прогноз должны вноситься соответствующие коррективы.
Коррективы могут быть различного уровня значимости, сложности, трудоемкости и т. д. Если они не очень значительны, то эта проблема может решаться на уровне аналитической группы, сопровождающей разработкой прогноза.
Если коррективы более существенны, то может потребоваться дополнительное привлечение отдельных экспертов, а в особо важных случаях при наличии значительных изменений – дополнительная работа экспертной комиссии с возможным изменением состава.
Структура прогноза обусловлена сроками, на которые он рассчитан, а также основными направлениями научно-технического развития, которые прежде всего зависят от «срока жизни» тенденций, сложившихся в пери-од, предшествующих их разработке. Чем более устойчивый характер носят эти тенденции, тем шире может быть горизонт прогнозирования. Различные воспроизводственные процессы имеют разные скорости протекания, разные временные циклы. Цикл воспроизводства приборов значительно короче цикла производства станков и другого оборудования, сроки обновления продукции машиностроения в значительной мере определяются динамикой технического уровня орудий труда.
Прогноз является предплановым документом и поэтому его внедрение на практике означает разработку научно-обоснованной стратегии фирмы, бизнес-план на основе использования вариантов прогноза показателей качества, затрат на его достижение и другой информации.
Прогнозирование управленческих решений преследует цель получения научно-обоснованных альтернатив развития для различных показателей, которые используются в НИОКР, а также для развития всей системы менеджмента. Получается, что прогнозирование управленческих решений есть часть системы менеджмента и способствует развитию всей системы в целом.
Но ЛПР должен помнить, что только решения и планы бывают идеальными, а люди и обстоятельства всегда реальны, и поэтому каждое управленческое решение, каждый план несет в себе возможность не только успеха, но и неудачи.
Контрольные вопросы
1. Дайте определения понятиям «прогноз» и «прогнозирование».
2. Какие источники неопределенности выделяют при прогнозировании УР?
3. Каковы основные задачи прогнозирования УР?
4. Какие выделяют источники информации при прогнозировании УР?
5. Охарактеризуйте методы и принципы прогнозирования УР.
6. Какие выделяют этапы прогнозирования УР?
7. Дайте характеристику этапам прогнозирования УР.
Существующие, приборы, системы и традиционные методы определения места судна имеют значительные недостатки. Так, например, погрешности определения счислимых координат зависят от точности работы лага и компаса, от гидрометеорологических условий "плавания, "погрешности определения счислимых координат растут с течением времени. Методы мореходной астрономии зависят от погодных условий, имеют ограниченную точность, а также требуют значительного времени для получения обсервованных координат. Визуальные методы определения места судна имеют ограниченный район применения, и их использование также зависит от погодных условий. Радиопеленгование имеет ограниченный район использования и низкую точность. Почти все радионавигационные системы имеют ограниченный район использования, а глобальные радионавигационные системы имеют и низкую точность. Спутниковые навигационные системы на низких орбитах обладают значительной дискретностью определения места. Радиолокационные станции имеют ограниченный район использования и необходимость опознания ориентиров.
Список можно продолжить, но уже совершенно очевидно, что недостатки традиционных методов и средств определения места судна в значительной мере снижают безопасность мореплавания.
1.6 Априорная и апостериорная оценка точности обсервации.
В соответствии с хорошей практикой любой инженерный расчет должен сопровождаться оценкой точности полученного результата: отыскание математического ожидания искомых параметров и их дисперсии. В судовождении при определении места судна рассчитывают координаты и оценивают их точность либо через ковариационную матрицу, либо через одну из ее геометрических интерпретаций, например в виде эллипса погрешностей.
Измерения проводятся с погрешностями, поэтому и обсервованные координаты вычисляются тоже с погрешностями.
1.6.1 Правило переноса погрешностей
Особенностью определения координат является тот факт, что измерения косвенные, то есть измеряются навигационные параметры, и допущенные погрешности затем переносятся в погрешности координат.
1.6.2 Априорная оценка точности обсервации
Для оценки точности обсервации используются вероятно-статистические методы, которые устанавливают границы некоторой доверительной области, в которой с заданной вероятностью может находиться истинное место судна. При этом делаются следующие допущения:
- В измерениях отсутствуют промахи, т.е. грубые погрешности;
- Систематические погрешности измерений определены и компенсированы поправкой;
- Вычислительные погрешности и погрешности графики пренебрежительно малы;
- Статистические числовые характеристики погрешностей измерений (дисперсия и СКП) и законы их распределения заданы априорно, т.е. по результатам предыдущих экспериментов (обсерваций). Эти априорные данные имеют приближенные средние значения и базируются на том, что все эксперименты, проведенные ранее с такими же приборами на судах, имеют сходные условия, что и текущая обсервация.
Рассмотрим этот вопрос на примере ОМС по двум измерениям. В этом случае линеаризованная система принимает вид.
A D X = D U (75)
Так как измерения с погрешностями, то перепишем систему в виде
A (D X+ d x) = D U+ d u. (76)
Тогда
A d x = d u.
Откуда
d x = A -1 d u. (77)
Погрешности измерений могут быть статистически зависимы. Такая зависимость существует хотя бы потому, что обычно используются как минимум одни и те же инструменты. Эта статистическая зависимость определяется коэффициентом корреляции, а общее описание такой зависимости дает ковариационная матрица погрешностей измерений.
Формирование ковариационной матрицы погрешности измерений выполняется по формуле
D(D u)= d u d u T . (78)
Для двумерного случая это выглядит так:
На главной диагонали находятся дисперсии измеряемых навигационных параметров, а вне диагонали - ковариационные моменты, которые характеризуют статистическую связь между измерениями.
Структура ковариационной матрицы погрешностей измерений определяет название МНК: если матрица диагональна и все ее компоненты равны, то алгоритм носит название МНК, если компоненты не равны, то это метод взвешенных наименьших квадратов; если матрица не диагональна, то это обобщенный МНК.
Погрешности измерений в процедуре расчета трансформируются в погрешности координат. В качестве такого преобразователя погрешностей используется матрица коэффициентов A.
Определим ковариационную матрицу погрешностей определяемых параметров, используя правила (A B) -1 = B -1 A -1 и (B -1) T =(B T) -1
D(D x)= d x d x T = (A -1 d u) (A -1 d u) T =A -1 d u d u T (A -1) T =
A -1 D(D u) (A -1) T = (A Т (D(D u)) -1 A) -1 .
В дальнейшем при написании ковариационных матриц, где это не вносит двузначности, будем опускать аргумент
Обозначим ковариационную матрицу погрешностей координат через
N= D(D x) = (A Т D -1 A) -1 . (79)
Для двумерного случая матрица N имеет вид:
 ,
,
где n 11 - дисперсия по широте
n 22 - дисперсия по отшествию.
n 12 = n 21 - ковариационные моменты.
Вся информация о погрешностях содержится в матрице N . В судовождении часто используется ее геометрическая интерпретация в виде эллипса погрешностей. Установим связь между элементами матрицы N и параметрами эллипса: полуосями и углом ориентации.
В общем случае такая задача рассматривалась Хоттелингом Г. в 1933 г. Было показано, что для ковариационной матрицы существуют векторы, направлениям которых соответствуют максимальные и минимальные значения рассеивания (погрешностей). Численно эти значения соответствуют собственным числам матрицы. Направления собственных векторов, указывающие на направление максимального и минимального рассеивания (дисперсии), соответствуют направлениям полуосей эллипса. Собственные числа - это экстремальные значения дисперсий. Для перехода к линейным величинам - полуосям эллипса (гипер - эллипса для n-мерного пространства), необходимо извлечь квадратный корень.
Априорная оценка точности измеряемых навигационных параметров основана на многочисленных статистических исследованиях, которые происходили до конкретной обсервации. В качестве основного параметра для априорной оценки точности измеряемых величин применяется средняя квадратическая погрешность измеряемого навигационного параметра т.
Особенностью определения координат является тот Аакт, что измерения -косвенные, т.е. измеряются навигационные параметры и допущенные погрешности затем переносятся в погрешности координат. Рассмотрим процедуру переноса погрешностей измерений в погрешности координат на примере ОМС по двум измерениям.
В этом случае линеаризованная система принимает вид: ;
Так как измерения имеют погрешности, то перепишем систему в виде
Формирование ковариационной матрицы погрешности измерений выполняется по формуле
![]()
где D - обозначение ковариационной.
Для двумерного случая выражение (2.24) выглядит так:
а операция математического ожидания, выполненная с матрицей 8U6U , превращает ее в ковариационную матрицу D,
![]()
На главной диагонали D находятся дисперсии.измеряемых навигационных параметров, а вне диагонали - ковариационные моменты, которые характеризуют статистическую связь между измерениями.
Аналогично определим ковариационную матрицу погрешностей искомых параметров, используя правила матричного исчисления (ABY l =B~ \ A~ \ и (Д- 1)-^^)- 1 .
N = D(A^) = D(SXSX 7) = D^A-"SU^A^SUY] = (A"D^A)^. (2.25)
В дальнейшем при написании ковариационных матриц, где это не вносит двузначности, будем опускать аргумент при D.
Для двумерного случая ковариационная матрица N имеет вид:
где п 11 - дисперсия погрешностей широты, n-г.г - дисперсия погрешностей отшест-вия, ni2 = пг\ - ковариационные моменты.
Вся информация о погрешностях содержится в матрице N. В судовождении часто используется ее геометрическая интерпретация в виде эллипса погрешностей. Установим - связь между элементами матрицы N и параметрами эллипса:
полуосями и углом ориентации.
В общем случае такая задача рассматривалась Г. Хоттелингом в 1933 г. Ученым было доказано, что для ковариационной матрицы существуют. векторы, направлениям которых соответствуют максимальные и минимальные значения рассеивания (погрешностей). Эти значения соответствуют собственным числам матрицы. Направления собственных векторов, указывающие на направление максимального и минимального рассеивания (дисперсии), соответствуют направлениям полуосей эллипса. Собственные числа - это экстремальные значения дисперсий. Для перехода к линейным величинам - полуосям эллипса (гиперэллипса для /7-мерного пространства), необходимо извлечь квадратный корень.
Рассмотрим эту задачу для двумерного случая, т.е. для плоскости. Физика и геометрия собственных чисел и векторов заключается в том, что результатом
умножения исходной матрицы на собственный вектор будет вектор, коллинеарный собственному, по длине отличающийся в число раз, пропорциональное собственному значению. Математически это запишется в виде:
Поставим численный эксперимент, который прояснит эту запись. Выполним умножение Nz, где в качестве z будем выбирать единичный вектор с направлением У от 0 до 360°. Формирование компонент единичного вектора
Компоненты вектора р (значения Х и У) приведены в табл. 2.1.
Таблица 2.1
| У | ^1 | Y | X | R |
| 8,13 | 21,000 | 3,000 | 21,213 | |
| 8,48 | 21,049 | 3,139 | 21,282 | |
| 8,83 | 21,092 | 3,277 | 21,345 | |
| 9,18 | 21,128 | 3,415 | 21,402 | |
| 9,53 | 21,158 | 3,551 | 21,454 | |
| 9,87 | 21,182 | 3,686 | 21,500 | |
| 10,22 | 21,199 | 3,820 | 21,540 | |
| 10,55 | 21,209 | 3,953 | 21,574 | |
| 10,90 | 21,213 | 4,084 | 21,603 | |
| 11,24 | 21,211 | 4,215 | 21,625 | |
| 11,58 | 21,202 | 4,344 | 21,642 | |
| 11,92 | 21,187 | 4,471 | 21,653 | |
| 12,26 | 21,165 | 4,598 | 21,658 | |
| 12,60 | 21,137 | 4,723 | 21,658 | |
| 12,93 | 21,102 | 4,846 | 21,651 | |
| 13,27 | 21,061 | 4,968 | 21,639 | |
| ... | ... | ... | ... | |
| 95,38 | -0,692 | 7,358 | 7,390 | |
| 98,30 | -1,062 | 7,281 | 7,358 | |
| 101,24 | -1,432 | 7,201 | 7,342 | |
| 104,19 | -1,801 | 7,120 | 7,344 | |
| 107,13 | -2,169 | 7,037 | 7,363 | |
| 110,05 | -2,537 | 6,951 | 7,400 | |
| 112,94 | -2,905 | 6,863 | 7,453 | |
| 115,72 | -3,271 | 6,113 | 7,522 |
В графе «У» указано направление единичного вектора z, в графе «Ti» -направление уже преобразованного вектора р. В графе «R» приведены значения длины вектора р. Из табличных данных видно, что расхождение в направлении вектора z и вектора р - величина переменная, но в районе 12° и 102° эти направления совпадают. Кроме того, им соответствуют максимальное и минимальное значение длины R. Таким образом, направления собственных векторов 12° и 102° - ортогональны. Собственные значения равны приблизительно 21,658 и 7,342 соответственно.
Для двумерного случая можно получить простые формулы. Согласно выражению (2.26), запишем:
![]()
![]()
а также представим в матричном виде:
Формально получаем

Квадратное уравнение. Решая его относительно X и,
принимая во внимание, что п-ц = пц (т.к. матрица N симметрическая), получим

Подставив значения из матрицы (2.27), получим а] == 21,659; Л^ = 7,341. Эти значения практически совпали с максимальным и минимальным значениями, приведенными в табл. 2.1.
Определим ориентацию собственных векторов, соответствующих найденным собственным значениям. Считая ^ известным, подставим это значение в уравнения системы (2.28) и решим ее относительно zi и z:, учитывая, что z/ == cosfF), z-г = = sinCF).
Первое уравнение системы (2.28) будет выглядеть так:
Разделив в первом уравнении левую и правую часть на cos(T), получим:
 |

Подставив числовые значения, получим ^F = 12,388.
Таким образом, фактически получено направление большой полуоси эллипса У относительно норда. Если в уравнение (2.31) подставить другое значение Л, то получим направление малой полуоси, но так как они ортогональны, то практически это не требуется.
Для отыскания полуосей необходимо извлечь квадратные корни из собственных чисел
![]()
Когда говорят об оценке точности, то обычно добавляют слова априорная или апостериорная. Априорная - это оценка точности, выполненная по информации о погрешностях измерений, полученной ранее. Как правило, такая информация о точности измеряемых навигационных параметров основывается на многочисленных статистических исследованиях, которые происходили до конкретной обсервации в каких-либо осредненных условиях. Именно такая информация обычно содержится в ковариационной матрице погрешностей измерений, используемой при расчете координат. В формуле (2.18) она обозначена как D. Если погрешности измерений статистически независимы, то внедиагональные элементы равны нулю и матрица имеет вид:

Эти погрешности, в соответствии с правилом их переноса, формируют априорную ковариационную матрицу определяемых параметров.
Процедура построения эллипса погрешностей по ковариационной матрице сводится к следующим операциям:
Расчету собственных значений ^ по формуле (2.29);
Определению угла ориентации У по формуле (2.31);
Расчету полуоси по формулам (2.32).
На рис. 2.5 показана связь между элементами ковариационной матрицы и эллипсом. Отрезок, заключенный между касательной к эллипсу параллельной оси Y и самой осью, соответствует
| СКП по широте: |
Отрезок на оси Y,
отсекаемый вертикальной касательной, соответствует СКП по отшествию:
На рис. 2.5 также показана СКП обсервации М, которая рассчитывается как корень квадратный из следа ковариационной матрицы либо с помощью полуосей эллипса.