Оптимальные системы автоматического управления. Оптимальные системы. Задача оптимального управления

11.08.2019 По случаю потери кормильца

ОПТИМАЛЬНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Постановка задачи оптимизации управления

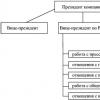
В общем случае автоматическая система состоит из объекта управления и совокупности устройств, которые обеспечивают управление этим объектом. Как правило, эта совокупность устройств включает в себя измерительные устройства, усилительные и преобразовательные устройства, а также исполнительные устройства. Если объединить эти устройство в одно звено (управляющее устройство), то структурная схема системы выглядит следующим образом:

В автоматической системе информация о состоянии объекта управления через измерительное устройство поступает на вход управляющего устройства. Такие системы называются системами с обратной связью или замкнутыми системами. Отсутствие этой информации в алгоритме управления говорит о том, что система разомкнута. Состояние объекта управления в любой момент времени будем описывать переменными , которые называются координатами системы или переменными состояния. Их удобно считать координатами - мерного вектора состояния .

Измерительное устройство выдает информацию о состоянии объекта. Если на основании измерения вектора могут быть найдены значения всех координат вектора состояния , то говорят, что система полностью наблюдаема.

Управляющее устройство вырабатывает управляющее воздействие . Таких управляющих воздействий может быть несколько, они образуют - мерный управляющий вектор .

На вход управляющего устройства поступает задающее входное воздействие . Это входное воздействие несет информацию о том, какое должно быть состояние объекта. На объект управления может действовать возмущающее воздействие , которое представляет собой нагрузку или помеху. Измерение координаты объекта, как правило, осуществляется с некоторыми погрешностями , которые тоже носят случайный характер.

Задачей управляющего устройства является выработка такого управляющего воздействия , чтобы качество функционирования автоматической системы в целом было бы наилучшим в некотором смысле.

Мы будем рассматривать такие объекты управления, которые являются управляемыми. То есть вектор состояния можно изменять требуемым образом путем соответствующего изменения вектора управления. Будем подразумевать, что объект полностью наблюдаемый.

Так, например, положение летательного аппарата характеризуется шестью координатами состояния. Это - координаты центра масс, - углы Эйлера, определяющие ориентацию летательного аппарата относительно центра масс. Положение летательного аппарата можно изменить с помощью рулей высоты, курса, элерона и с помощью уклонения вектора силы тяги. Таким образом управляющий вектор определен следующим образом:

Угол отклонения рулей высоты

Вектор состояния в этом случае определяется следующим образом:

Можно поставить задачу выбора управления, с помощью которого летательный аппарат переводится из заданного начального состояния в заданное конечное состояние с минимальными затратами топлива или за минимальное время.

Дополнительная сложность при решении технических задач возникает в силу того, что на управляющее воздействие и на координаты состояния объекта управления, как правило, накладываются различные ограничения.

На любой угол рулей высоты, курса, элерона существуют ограничения:

Тяга сама по себе ограничена.

На координаты состояния объекта управления и их производные также накладываются ограничения, которые связаны с допустимыми перегрузками.

Мы будем рассматривать объекты управления, которые описываются дифференциальным уравнением:

(1)

Или в векторном виде:

Мерный вектор состояния объекта

Мерный вектор управляющих воздействий

Функция правой части уравнения (1)

На вектор управления накладывается ограничение, мы будем полагать, что его значения принадлежат некоторой замкнутой области некоторого -мерного пространства. Это означает, что управляющая функция в любой момент времени принадлежит области ().

Так, например, если координаты управляющей функции удовлетворяет неравенствам:

то область является -мерным кубом.

Назовем допустимым управлением всякую кусочно-непрерывную функцию , значения которой в каждый момент времени принадлежит области , и которая может иметь разрывы первого рода. Оказывается, даже в некоторых задачах оптимального управления решение может быть получено в классе кусочно-непрерывного управления. Для того, чтобы выбрать управление как функцию времени и начального состояния системы , которое однозначно определяет движение объекта управления, требуется, чтобы система уравнений (1) удовлетворяла условиям теоремы существования и единственности решения в области . В этой области располагаются возможные траектории движения объекта и возможные управляющие функции . Если область изменения переменных является выпуклой, то для существования и единственности решения достаточно, чтобы функции . были непрерывны по всем аргументам и имели непрерывные частные производные по переменным .

В качестве критерия, который характеризует качество работы системы, выбирается функционал вида:

(2)

В качестве функции будем предполагать, что она непрерывна по всем своим аргументам и имеет непрерывные частные производные по .

Критерии оптимизации

В зависимости от вида подынтегральной функции функционала:

(1)

могут быть получены различные критерии применяемой проектируемой автоматической системой.

ОПТИМАЛЬНЫЕ И АДАПТИВНЫЕ СИСТЕМЫ

(лекции, заочный факультет, 5 курс)

Лекция 1.

Введение.

В классической теории автоматического управления (ТАУ) задачи оптимизации и адаптации ставились в основном применительно к управлению «в малом». Это означает, что оптимальная программа изменения режимов технологического процесса, выраженная в задающих воздействиях регуляторов, считалась известной, определенной на стадии проектирования. Задача управления заключалась в выполнении этой программы, стабилизации программного движения. При этом допускались лишь малые отклонения от заданного движения, и переходные процессы «в малом» оптимизировались по тем или иным критериям.

В конце 50-х - начале 60-х гг. XX столетия появились работы Л.С. Понтрягина (принцип максимума), Р. Беллмана (динамическое программирование), Р. Калмана (оптимальная фильтрация, управляемость и наблюдаемость), которые заложили основы современной теории автоматического управления, общепринятого определения понятия которой пока не существует.

Наиболее точно современную теорию автоматического управления можно отделить от классической ТАУ, учитывая требования научно-технического прогресса, современной и перспективной автоматизации. Важнейшим из таких требований является оптимальное использование всех располагаемых ресурсов (энергетических, информационных, вычислительных) для достижения главной обобщенной конечной цели при соблюдении ограничений.

Прежде всего указанная оптимизация требует полного использования имеющейся априорной информации в виде математической модели управляемого процесса или объекта. Использование таких моделей не только на стадии проектирования, но и в процессе функционирования систем, является одной из характерных черт современной теории автоматического управления.

Оптимальное управление возможно лишь при оптимальной обработке информации. Поэтому теория оптимального (и субоптимального) оценивания (фильтрации) динамических процессов является составной частью современной теории автоматического управления. Особо важной является параметрическая идентификация (оценивание параметров и характеристик по экспериментальным данным), выполняемая в реальном масштабе времени в эксплуатационных режимах ОУ.

Подлинная оптимизация автоматического управления в условиях неполной априорной информации возможна только в процессе функционирования системы в текущей обстановке и возникшей ситуации. Следовательно, современная теория автоматического управления должна рассматривать адаптивное оптимальное (субоптимальное) управление «в большом». Кроме того, современная теория автоматического управления должна рассматривать методы резервирования и структурного обеспечения надежности (особенно принципы автоматической реконфигурации системы при отказах).

Определение, особенности и общая характеристика оптимальных систем.

Оптимальной называется наилучшая в некотором технико-экономическом смысле система. Основной ее особенностью является наличие двух целей управления, которые эти системы решают автоматически.

Основная цель управления - поддержание управляемой величины на заданном значении и устранение возникающих отклонений этой величины.

Цель оптимизации - обеспечение наилучшего качества управления, определяемое по достижению экстремума некоторого технико-экономического показателя, называемого критерием оптимальности (КО).

Оптимальные системы разделяют в зависимости от вида КО на два класса: оптимальные в статике системы и оптимальные в динамике системы.

У оптимальных в статике систем КО является функцией параметров или управляющих воздействий. Этот критерий имеет экстремум в статическом режиме работы системы, причем статическая характеристика, выражающая зависимость КО от управляющих воздействий оптимизации, может непредвиденным образом смещаться под действием возмущений. Оптимальная система должна этот экстремум находить и поддерживать. Такие системы применимы, если возмущения, смещающие указанную характеристику, изменяются сравнительно медленно по сравнению с длительностью переходных процессов в системе. Тогда система будет успевать отслеживать экстремум практически в статическом режиме. Такие условия обычно выполняются на верхней ступени иерархии управления.

Оптимальные в динамике системы отличаются тем, что их критерий оптимальности представляет собой функционал, т. е. функцию от функций времени. Это значит, что, задав функции времени, от которых данный функционал зависит, получим числовое значение функционала. Эти системы могут применяться при сравнительно быстро меняющихся внешних воздействиях, не выходящих, однако, за допустимые пределы. Поэтому они используются на нижних уровнях управления.

1.2. Критерии оптимальности оптимальных в динамике систем

Обычно эти функционалы имеют вид определенных интегралов по времени

где x(t), u(t) - векторы состояния и управления данной системы;

Т - длительность процесса (в частности, может быть Т = ).

В зависимости от подынтегральной функции f 0 эти критерии имеют следующие основные виды.

1. Линейные функционалы, у которых f 0 - линейная функция переменных:

Критерий максимального быстродействия при f 0 1, т.е.

который равен длительности процесса, а соответствующие системы называют оптимальными по быстродействию;

Линейные интегральные оценки

Критерий максимальной производительности

где q(t) - количество произведенной продукции.

2. Квадратичные функционалы, у которых f 0 - квадратичная форма от входящих в нее переменных:

Квадратичные интегральные оценки качества переходного процесса

;

Критерий энергозатрат на управление, у которого

где u - управляющее воздействие, а и 2 - мощность, затрачиваемая на управление;

Обобщенный квадратичный критерий, равный сумме двух предшествующих, взятых с некоторыми весовыми коэффициентами. Он компромиссно характеризует качество переходного процесса и энергозатраты на него, т. е.

где Q и R - положительно определенные квадратные матрицы. Функционалы, не содержащие интегралов:

Критерий минимакса, при оптимизации по которому надо обеспечить минимальное значение максимума модуля (нормы) вектора отклонения управляемого процесса от его эталонного закона изменения, т. е.

, где x э – эталонный закон изменения.

Простейшим примером этого критерия для скалярного случая является известное максимальное перерегулирование переходного процесса;

Функция от конечного состояния

которая является функционалом потому, что конечное состояние объекта х (Т) является функцией от управляющего воздействия u (t). Этот критерий оптимальности может применяться в сумме с одним из рассмотренных выше критериев, имеющих вид определенного интеграла.

Выбор того или иного критерия оптимальности для конкретного объекта или системы производится на основании соответствующего изучения работы объекта и предъявляемых к нему требований технико-экономического характера. Этот вопрос не может быть решен в рамках только теории автоматического управления. В зависимости от физического смысла критерия оптимальности его требуется либо минимизировать, либо максимизировать. В первом случае он выражает потери, во втором случае технико-экономическую выгоду. Формально, поменяв знак перед функционалом, можно задачу по максимизации свести к задаче по минимизации.

Лекция 2.

1.3. Краевые условия и ограничения
для оптимальных в динамике систем

Основная цель управления в таких системах обычно формулируется как задача перевода изображающей точки из некоторого начального состояния х(О) в некоторое конечное х(Т) состояние. Начальное состояние принято называть левым концом оптимальной траектории, а конечное - правым. Вместе взятые эти данные и образуют краевые условия. Задачи управления могут отличаться видом краевых условий.

1. Задача с закрепленными концами траектории имеет место, когда х (0) и х (Т) фиксированные точки пространства.

2. Задача с подвижными концами траектории получается, когда х (0) и х (Т) принадлежат некоторым известным линиям или поверхностям пространства.

3. Задача со свободными концами траектории возникает, когда указанные точки занимают произвольные положения. На практике встречаются и смешанные задачи, например х (0) - фиксирован, а х (Т) подвижен. Такая задача будет иметь место, если объект из заданного фиксированного состояния должен «догнать» некоторую эталонную траекторию (рис. 1).

Ограничениями называются дополнительные условия, которым должны удовлетворять управляющие воздействия и управляемые величины. Встречаются два вида ограничений.

1. Безусловные (естественные) ограничения, которые выполняются в силу физических законов для процессов в объекте управления (ОУ). Эти ограничения показывают, что некоторые величины и их функции не могут выйти за границы, определяемые равенствами или неравенствами. Например, уравнение двигателя постоянного тока (ДПТ):

ограничение на скорость асинхронного двигателя , где - синхронная скорость.

2. Условные (искусственные) ограничения, выражающие такие требования к величинам или функциям от них, согласно которым они не должны превосходить границ, определенных равенствами или неравенствами по условиям долговечной и безопасной эксплуатации объектов. Например, ограничение на питающее напряжение , ограничения на допустимую скорость, ускорение и т. п.

Для обеспечения условных ограничений необходимо принимать меры схемного или программного характера при реализации соответствующего управляющего устройства.

Ограничения, независимо от их вида, выражаемые равенствами, называются классическими, а неравенствами - неклассическими.

Похожая информация.

Системы автоматического регулирования обычно проектируют, исходя из требований обеспечения тех или иных показателей качества. Во многих случаях необходимое повышение динамической точности и улучшение переходных процессов автоматических систем достигается с помощью корректирующих устройств.

Особенно широкие возможности повышения показателей качества дает введение в схему автоматической системы разомкнутых компенсационных каналов и дифференциальных связей, синтезированных из тoгo или иного условия инвариантности ошибки относительно задающего или возмущающих воздействий. Однако эффект влияния корректирующих устройств, разомкнутых компенсационных каналов и эквивалентных им дифференциальных связей на показатели качества работы автоматической системы зависит от уровня ограничения сигналов нелинейными элементами системы. Выходные сигналы дифференцирующих устройств, обычно кратковременные по длительности и значительные по амплитуде, ограничиваются элементами системы и не приводят к улучшению показателей качества автоматической системы, в частности ее быстродействия. Лучшие результаты решения задачи повышения показателей качества автоматических систем при наличии ограничений сигнала дает так называемое оптимальное управление.

В широком значении слово «оптимальный» означает наилучший в смысле некоторого критерия эффективности. При таком толковании любая научно обоснованная технико-экономическая система является оптимальной, так как при выборе какой-либо системы подразумевается, что она в каком-либо отношении лучше других. Критерии, с помощью которых осуществляется выбор (критерии оптимальности), могут быть различными. Этими критериями могут являться качество динамики процессов управления, надежность системы, энергопотребление, ее вес и габариты, стоимость и т. п., либо совокупность этих критериев с некоторыми весовыми коэффициентами . Во многих случаях необходимое повышение динамической точности и улучшение переходных процессов систем автоматического регулирования достигается с помощью корректирующих устройств.

Особенно широкие возможности повышения показателей качества дает введение в автоматические системы разомкнутых компенсационных каналов и дифференциальных связей, синтезированных из того или иного условия инвариантности ошибки относительно задающего или возмущающих воздействий. Однако эффект влияния корректирующих устройств, разомкнутых компенсационных каналов и эквивалентных им дифференциальных связей на показатели качества работы автоматических систем зависит от уровня ограничения сигналов нелинейными элементами системы. Выходные сигналы дифференцирующих устройств, обычно кратковременные по длительности и значительные по амплитуде, ограничиваются элементами системы и не приводят к улучшению показателей качества работы автоматической системы, в частности ее быстродействия. Лучшие результаты решения задачи повышения показателей качества работы автоматических систем при наличии ограничений сигнала дает так называемое оптимальное управление.

Задача синтеза оптимальных систем стpoгo сформулирована сравнительно недавно, Когда было дано определение понятия критерия оптимальности. В качестве критерия оптимальности в зависимости от цели управления мoгут быть выбраны различные технические или экономические показатели управляемого процесса. В оптимальных автоматических системах обеспечивается не просто некоторое повышение того или иного технико-экономического показателя качества, а достижение минимально или максимально возможного eгo значения.

Оптимальным называется управление, осуществляемое наилучшим по определенным показателям образом. Системы, реализующие оптимальное управление, называются оптимальными. Opгaнизация оптимального управления основана на выявлении и peaлизации предельных возможностей систем.

При разработке систем оптимального управления одним из важнейших шагов является формулировка критерия оптимальности, под которым понимается основной показатель, определяющий задачу оптимизации. Именно по этому критерию оптимальная система должна функционировать наилучшим образом.

В качестве критериев оптимальности выступают разнообразные технические и технико-экономические показатели, выражающие технико-экономическую выгоду или, наоборот, потери. В силу противоречивости требований, предъявляемых к системам автоматического управления, выбор критерия оптимальности обычно превращается в сложную задачу, имеющую неоднозначное решение. Например, оптимизация автоматической системы по критерию надежности может повлечь за собой увеличение стоимости системы, ее усложнение. С другой стороны, упрощение системы снизит ряд других ее показателей. К тому же, не всякое оптимальное решение, синтезированное теоретически, можно реализовать на практике на базе достигаемого уровня техники.

В теории автоматического регулирования используются функционалы, характеризующие отдельные показатели качества. Поэтому чaще вceгo оптимальные автоматические системы синтезируется оптимальным по какому-то одному основному критерию, а остальные показатели, определяющие качество функционирования автоматической системы, ограничиваются областью допустимых значений. Это упрощает и делает более определенной задачу поиска оптимальных решений при разработке оптимальных систем.

Вместе с тем усложняется задача выбора конкурирующих вариантов систем, так как они сравниваются по различным критериям, а оценка системы не имеет однозначного ответа. Действительно, без тщательного анализа множества противоречивых, зачастую неформализуемых факторов трудно ответить, например, на такой вопрос какая из систем лучше: более надежная или менее дорогая?

Если критерий оптимальности выражает технико-экономические потери (ошибки автоматической системы, время переходного процесса, расход энергии, средств, стоимость и т. п), то оптимальным будет такое: управление, которое обеспечивает минимум критерия оптимальности. Если же он выражает рентабельность (к. п.д., производительность, прибыль,
дальность полета ракеты и т. д.), то оптимальное управление должно обеспечить максимум критерия оптимальности.

Задача определения оптимальной автоматической системы, в частности синтез оптимальных параметров автоматической системы при поступлении на ее вход задающего воздействия и помехи, являющихся стационарными случайными сигналами, в качестве критерия оптимальности принято среднеквадратическое значение ошибки. Условия повышения точности воспроизведения полезного сигнала (задающего воздействия) и подавления помехи носят противоречивый характер, и поэтому возникает задача выбора таких (оптимальных) параметров системы, при которых среднеквадратическая ошибка принимает наименьшее значение.

Синтез оптимальной системы при среднеквадратическом критерии оптимальности является частной задачей. Общие методы синтеза оптимальных систем основываются на вариационном исчислении. Oднако классические методы вариационного исчисления для решения современных практических задач, требующих учета ограничений, во многих случаях оказываются непригодными. Наиболее удобными мeтодами синтеза оптимальных систем автоматического управления являются метод динамического программирования Беллмана и принцип максимума Понтрягина.

В общем процессе проектирования технических систем можно видеть проблемы двух типов.
1 Проектирование системы управления, направленной на достижение поставленной задачи (формирование траекторий, режимов, выбор методов управления , реализующих траектории и т. д.). Этот круг задач можно назвать проектированием движений.
2 Проектирование конструктивных и прочностных схем (выбор геометрических, аэродинамических, конструктивных и других параметров), обеспечивающих выполнение общих характеристик и конкретных режимов работы. Этот круг задач проектирования связан с выбором ресурсов, необходимых для реализации поставленных задач.

Проектирование движений (изменение технологических параметров) тесно связано с группой проблем второго типа, так как получаемая при проектировании движений информация является исходной (во многом определяющей) для решения этих проблем. Но и в тех случаях, когда имеется уже готовая техническая система (т. е. располагаемые ресурсы определены), в процессе его модификации могут быть осуществлены оптимизирующие приемы.

Проблемы первого типа решаются в настоящий момент наиболее эффективно и строго на основе общих методов математической теории оптимальных процессов управления. Значение математической теории оптимальных процессов управления заключается в том, что она дает единую методологию решения весьма широкого круга задач оптимального проектирования и управления, устраняет инерции и недостаточную общность прежних частных методов и способствует ценными результатами и методами, полученными в смежных областях.

Теория оптимальных процессов позволяет решать широкий круг практических задач в достаточно общей постановке с учетом большинства ограничений технического характера, накладываемых на осуществимость технологических процессов. Роль методов теории оптимальных процессов особенно возросла в последние годы в связи с широким внедрением в процесс проектирования ЭВМ.

Таким образом, наряду с проблемой улучшения различных показателей качества работы автоматической системы возникает задача построения оптимальных автоматических систем, в которых достигается экстремальное значение того или иного технико-экономического показателя качества.

Разработка и внедрение оптимальных систем автоматического управления способствует повышению эффективности использования производственных aгpeгaтов, увеличению производительности труда, улучшению качества продукции, экономии электроэнергии, топлива, сырья и т. п.

Оптимальные системы классифицируются по различным признакам. Отметим некоторые из них.
В зависимости от реализуемого критерия оптимальности различают:
1) системы, оптимальные по быстродействию. Они реализуют критерий минимального времени переходных процессов;
2) системы, оптимальные по точности. Они формируются по критерию минимума отклонения переменных за время переходных процессов или по критерию минимума среднеквадратичной ошибки;
3) системы, оптимальные по расходу топлива, энергии и т. д., реализующие критерий минимума расхода;
4) системы, оптимальные по условиям инвариантности. Они синтезируются по критерию независимости выходных переменных от внешних возмущений или от других переменных;
5) оптимальные экстремальные системы, обусловливающие критерий минимума отклонения показателя качества от eгo экстремального значения.

В зависимости от характеристик объектов оптимальные системы подразделяются на:
1) линейные системы;
2) нелинейные системы;
3) непрерывные системы;
4) дискретные системы;
5) аддитивные системы;
6) параметрические системы.

Эти признаки, кроме двух последних, не нуждаются в пояснениях. В аддитивных системах воздействия на объект не изменяют eгo xapaктеристик. Если же воздействия изменяют коэффициенты уравнений объекта, то такие системы называются параметрическим.

В зависимости от типа критерия оптимальности оптимальные системы подразделяются на следующие:
1) равномерно оптимальные, в которых каждый отдельный процесс протекает оптимально;
2) статистически оптимальные, реализующие критерий оптимальности, имеющий статистический характер из-за случайных воздействий на систему. В этих системах наилучшее поведение обеспечивается не в каждом отдельном процессе, а лишь в некоторых. Статистически оптимальные системы можно назвать оптимальными в среднем;
3) минимаксно оптимальные, которые синтезируются из условия минимаксного критерия, обеспечивающего лучшим наихудший результат по сравнению с подобным наихудшим результатом в любой другой автоматической системе.

По степени полноты информации об объекте оптимальные системы подразделяются на системы с полной и нe полной информацией. В состав информации об объекте включаются сведения:
1) о зависимости между входными и выходными вeличинами объекта;
2) о состоянии объекта;
3) о задающем воздействии, определяющем требуемый режим работы системы;
4) о цели управления функционале, выражающем критерий оптимальности;
5) о характере возмущения.

Информация об объекте в действительности всегда неполная, однако во многих случаях это не оказывает существенного влияния на функционирование системы по избранному критерию оптимальности. В ряде же случаев неполнота информации настолько существенна, что при решении задач оптимального управления требуется использование статистических методов.

В зависимости от полноты информации от объекте управления критерий оптимальности может быть выбран «жестким» (при дoстаточно полной информации) или «приспосабливающимся», т. е. изменяющимся при изменении информации. По этому признаку оптимальные системы подразделяются на системы с жесткой нaстройкой и адаптивные. В число адаптивных систем входят экстремальные, самонастраивающиеся и обучающиеся системы. Эти системы наиболее полно отвечают современным требованиям, предъявляемым к системам оптимального управления.

Решение задачи синтеза оптимальной системы заключается в разработке системы управления, отвечающей заданным требованиям, т. е. в создании системы, реализующей выбранный критерий оптимальности. В зависимости от объема сведений о структуре автоматической системы управления задача синтеза ставится в одной из двух следующих постановок.

Первая постановка охватывает случаи, когда структура автоматической системы известна. В таких. случаях объект и регулятор могут быть описаны соответствующими передаточными функциями, а задача синтеза сводится к определению оптимальных значений числовых параметров всех элементов системы, т. е. таких параметров, которые обеспечивают реализацию выбранного критерия оптимальности.

Во второй постановке задача синтеза ставится при неизвестной структуре системы. В этом случае требуется определить такую структуру и такие параметры системы, которые обеспечат систему, оптимальную по принятому критерию качества. В инженерной практике задача синтеза в такой постановке встречается редко. Чаще вceгo объект управления либо задан как физическое устройство, либо описан математически, и задача синтеза сводится к синтезу оптимального регулятора. Следует подчеркнуть, что и в этом случае необходим системный подход к синтезу системы оптимальнoгo управления. Суть такого подхода заключается в том, что при синтезе регулятора рассматривается вся система (регулятор и объект) как единое целое.

На начальной стадии синтеза оптимального регулятора задача сводится к eгo аналитическому конструированию, т. е. к определению eгo математического описания. При этом одну и ту же мaтематическую модель регулятора можно реализовать различными физическими устройствами. Выбор конкретной физической реализации аналитически определенного регулятора осуществляется с учетом условий работы конкретной системы автоматического управления. Таким образом, задача синтеза оптимального регулятора неоднозначна и может быть решена различными путями.

При синтезе системы оптимального управления весьма важно создание модели объекта, максимально адекватной реальному объекту. В теории управления так же, как в других современных областях науки, основными видами моделей объектов являются математические модели уравнения статики и динамики объектов.

При решении задач синтеза оптимальной системы единой мaтематической моделью объектов управления обычно является модель в форме уравнений состояния. Под состоянием системы aвтоматического управления в каждый момент времени понимается минимальный набор переменных (переменных состояния), который содержит. количество информации, достаточное для определения координат системы в текущем и будущем состояниях системы. Исходные уравнения объекта обычно нелинейны. Для приведения их к форме уравнений состояний широко используются методы линейных преобразований исходных уравнений.

Постановка основных задач оптимального управления в форме временной программы для автоматической системы с критерием оптимальности и краевыми условиями формулируется следующим образом.

Среди всех допустимых на отрезке программных управлений u = u(t) и управляющих параметров, переводящих точку (t0, x0) в точку (t1, x1) , найти такие, для которых функционал на решениях системы уравнений примет наименьшее (наибольшее) значение с выполнением условий оптимальности.

Управление u(t), решающее эту задачу, называется оптимальным (программным) управлением, а вектор а – оптимальным параметром. Если пара {u*(t), a*} доставляет абсолютный минимум функционалу I на решениях системы, то выполняется соотношение

Основная задача оптимального координатного управления известна в теории оптимальных процессов как проблема синтеза оптимального закона управления, а в некоторых задачах – как задача об оптимальном законе поведения.

Задача синтеза оптимального закона управления для системы с критерием и краевыми условиями, где для упрощения предполагается, что функции f0, f, h, g от вектора а не зависят, формулируется следующим образом.

Среди всех допустимых законов управления v(x, t) найти такой, что для любых начальных условий (t0, x0) при подстановке этого закона осуществляется заданный переход и критерий качества I[u] принимает наименьшее (наибольшее) решение.

Траектория движения автоматической системы, соответствующая оптимальному управлению u*(t) или оптимальному закону v*(x, t), называется оптимальной траекторией. Совокупность оптимальных траекторий x*(t) и оптимального управления u*(t) образует оптимальный управляемый процесс {x*(t), u*(t)}.

Так как закон оптимального управления v*(x, t) имеет форму закона управления с обратной связью, то он остается оптимальным для любых значений начальных условий (t0, x0) и любых координат x. В отличие от закона v*(x, t)программное оптимальное управление u*(t) является оптимальным лишь для тех начальных условий, для которых оно было вычислено. При изменении начальных условий будет меняться и функция u*(t). В этом состоит важное, с точки зрения практической реализации системы автоматического управления, отличие закона оптимального управления v*(x, t) от программного оптимального управления u*(t), поскольку выбор начальных условий на практике никогда не может быть сделан абсолютно точно.

Всякая часть оптимальной траектории (оптимального управления) также в свою очередь является оптимальной траекторией (оптимальным управлением). Это свойство математически формулируется следующим образом.

Пусть u*(t), t0 < t < t1, – оптимальное управление для выбранного функционала I[u], соответствующее переходу из состояния (t0, x0) в состояние (t1, x1) по оптимальной траектории x*(t). Числа (t0, t1) и вектор x0 – фиксированные, а вектор x1 , вообще говоря, свободен. На оптимальной траектории x*(t) выбираются точки x*(t0) и x*(t1), соответствующие моментам времени t = t0, t = t1. Тогда управление u*(t) на отрезке является оптимальным, соответствующим переходу из состояния x*(t0) в состояние x*(t1), а дуга является оптимальной траекторией

Таким образом, если начальное состояние системы есть x*(t0) и начальный момент времени t = t0, то независимо от того, каким образом пришла система к этому состоянию, ее оптимальным последующим движением будет дуга траектории x*(t), t0 < t < t1, являющейся частью оптимальной траектории между точками(t0, x0) и (t1, x1). Это условие является необходимым и достаточным свойством оптимальности процесса и служит основой динамического программирования.

Математическое описание задачи перевода объекта регулирования (процесса) из одного состояния в другое характеризуется n фазовыми координатами x1, x2, x3, . . . xn. При этом к объекту автоматического регулирования может быть приложено г управляющих воздействий u1, u2, u3, . . . uг.

Управляющие воздействия u1(t), u2(t), u3(t), . . . uг(t)удобно считать координатами некоторого вектора u = (u1, u2, u3, . . . uг), называемого вектором управляющего воздействия. Фазовые координаты (переменные состояния) объекта регулирования х1, х2, х3, . . . хn также можно рассматривать как координаты некоторого вектора или точки с координатами х = (х1, х2, х3, . . . хn) в n-мерном пространстве состояний. Эту точку называют фазовым состоянием объекта, а n-мерное пространство, в котором в виде точек изображаются фазовые состояния, называется фазовым пространством (пространством состояний) рассматриваемого объекта. При использовании векторных изображений управляемый объект можно изобразить как показано на рисунке. Под влиянием управляющего воздействия u (u1, u2, u3, . . . uг) фазовая точка х (х1, х2, х3, . . . хn) перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движения объекта регулирования.

Зная управляющее воздействие u(t) = u1(t), u2(t), u3(t), . . . uг(t), можно при наличии возмущений однозначно определить движение объекта регулирования при t > t0 , если известно его начальное состояние при t = t0 . Если изменить управление u(t), то движение точки будет происходить по другой траектории, т. е. для разных управлений получаем разные траектории, исходящие из одной точки. Поэтому переход объекта из начального фазового состоянияхH в конечное хK можно осуществить по разным фазовым траекториям в зависимости от управления. Среди множества траекторий существует наилучшая в определенном смысле, т. е. оптимальная траектория. Например, если поставлена задача минимального расхода топлива в течение интервала движения локомотива, то следует подойти к выбору управления и соответствующей траектории именно с этой точки зрения. Удельный расход топлива g зависит от развиваемой силы тяги управляющего воздействия u(t), т. е. g (t). Критерий оптимальности обычно представляется в виде некоторого функционала.

Задача синтеза оптимальных автоматических систем стpoгo сформулирована сравнительно недавно, Когда было дано определение понятия критерия оптимальности. В качестве критерия оптимальности в зависимости от цели управления могут быть выбраны различные технические или экономические показатели управляемого процесса. В оптимальных системах обеспечивается не просто некоторое повышение тoгo или иного технико-экономического показателя качества, а достижение минимально или максимально возможного eгo значения.

Важным шагом в постановке и решении общей задачи управления является выбор критерия оптимальности. Этот выбор является неформальным актом, он не может быть предписан какой-либо теорией, а целиком определяется содержанием задачи. В некоторых случаях формальное выражение понимания оптимальности системы допускает несколько эквивалентных (или почти эквивалентных) формулировок.

Если критерий оптимальности выражает технико-экономические потери (ошибки системы, время переходного процесса, расход энергии, средств, стоимость и т. п), то оптимальным будет такое: управление, которое обеспечивает минимум критерия оптимальности. Если же он выражает рентабельность (к. п.д., производительность, прибыль, дальность полета ракеты и т. д.), то оптимальное управление должно обеспечить максимум критерия оптимальности.

В таких случаях успех и простота получаемого решения во многом определяется выбранной формой критерия оптимальности (при условии, что во всех случаях он достаточно полно определяет требования задачи к системе). После построения математической модели процесса управления дальнейшее ее исследование и оптимизация проводится математическими методами . Оптимальное поведение или состояние автоматической системы обеспечивается тогда, когда функционал достигает своего экстремума I = extг максимума или минимума, в зависимости от физического смысла переменных.

В практике разработки и исследования динамических систем наиболее часто встречаются две задачи:
1) синтез системы, оптимальной по быстродействию;
2) синтез системы, оптимальной по точности.

В первом случае необходимо обеспечить минимум вpeмени переходного процесса, во втором минимум cpеднеквадратичной ошибки (отклонения координаты Dyi (t) от заданного значения) при заданных или случайных воздействиях.

Функционал в таком случае можно определить как функцию, аргументы которой связаны с критериями оптимальности и сами являются функциями переменных. Интересующий нас суммарный расход топлива основной в данном случае показатель качества систем управления движением локомотива определяется интегральным функционалом.

Интегральный функционал, характеризующий основной показатель качества автоматической системы (в рассматриваемом примере расход топлива), называется критерием оптимальности. Каждому управлению u(t), а следовательно, траектории движения локомотива соответствует свое числовое значение критерия оптимальности. Возникает задача выбора такого управления u(t) и траектории движения х(t), при которых достигается минимальное значение критерия оптимальности.

Обычно используются критерии оптимальности, величина которых определяется не текущим состоянием объекта (в рассматриваемом примере удельным расходом топлива), а изменением eгo в течение вceгo процесса управления. Поэтому для определения критерия оптимальности требуется, как и в приведенном примере, интегрировать какую-либо функцию, величина которой в общем случае зависит от текущих значений фазовых координат х объекта и управляющегоu, воздействия, т. е. такой критерий оптимальности является интегральным функционалом вида

В тех случаях, когда фазовые координаты объекта представляют стационарные случайные функции, критерий оптимальности представляет собой интегральный функционал не во временной, а в частотной области. Такие критерии оптимальности используются при решении задачи оптимизации систем по минимуму дисперсии ошибки. В простейших случаях критерий оптимальности может представлять собой не интегральный функционал, а просто функцию.

В теории автоматического регулирования используются так называемые минимаксные критерии оптимальности, характеризующие условия наилучшей работы системы в наихудших возможных условиях. Примером использования минимаксного критерия может быть выбор на eгo основе варианта системы автоматического управления, имеющей минимальное значение максимального перерегулирования. Любой критерий оптимальности реализуется при наличии ограничений, накладываемых на переменные и на показатели качества управления. В системах автоматического регулирования ограничения, накладываемые на координаты управления, можно подразделить на естественные и условные.

Во многих случаях к автоматической системе предъявляются противоречивые требования (например, требования минимума расхода топлива и максимальной скорости движения поезда). При выборе управления, отвечающего одному требованию (критерию минимума расхода топлива), не будут удовлетворяться другие требования (максимальная скорости движения). Поэтому из всех требований выбора одно основное, которое должно удовлетворяться наилучшим образом, а другие требования учитываются в виде ограничений их значений. Например, при удовлетворении требования минимального расхода топлива oгpaничивается минимальное значение скорости движения. Если имеются несколько равных показателей качества, которые не удается объединить в общий комбинированный показатель, выбор оптимальныx управлений, соответствующих этим показателям в отдельности при ограничении остальных дает варианты решения, которые могут (при проектировании) помочь при выборе оптимального компромисснoгo варианта.

При выборе управляющего воздействия u следует иметь ввиду, что оно не может принимать произвольные значения, так как на него наложены реальные ограничения, определяемые техническими условиями. Например, значение управляющего напряжения, подаваемого на электродвигатель, ограничено eгo предельным значением, определенным условиями эксплуатации электродвигателя.

Оптимальное управление может быть достигнуто, если объект является управляемым, т. е. существует хотя бы одно допустимое управление, переводящее объект из начального состояния в заданное конечное. Требование минимизации критерия оптимальности может быть формально заменено требованием минимизации конечного значения одной из координат объекта управления.

Если граничные условия в задаче оптимального управления заданы начальной и конечной точками траектории, то имеем задачу с фиксированными концами, В том случае, кoгдa одно или оба граничных условия заданы не точкой, а конечной областью или совсем не заданы. то имеем задачу со свободными концами или одним свободным концом. Примером задачи с одним свободным концом является задача устранения отклонения в системе автоматического управления, вызванного скачкообразным изменением задающего или возмущающего воздействия.

Важным частным случаем оптимального управления является задача об оптимальном быстродействии. Среди всех допустимых управлений u(t), под воздействием которых объект регулирования переходит из начального фазового состояния хH в заданное конечное состояние хK, найти такое, для которогo этот переход осуществляется за кратчайшее время.

Теория оптимальных процессов является основой единой методологии проектирования оптимальных движений, технических, экономических и информационных систем . В результате применения методов теории оптимальных процессов к задачам конструирования различных систем могут быть получены:
1) оптимальные по тому или иному критерию временные программы изменения управляющих воздействий и оптимальные значения постоянных управляющих (проектных, настроечных) параметров с учетом различного рода ограничений на их значения;
2) оптимальные траектории, режимы с учетом ограничений на область их расположения;
3) оптимальные законы управления в форме обратной связи, определяющие структуру контура системы управления (решение задачи синтеза управления);
4) предельные значения ряда характеристик или иных критериев качества, которые затем можно использовать как эталон для сравнения с другими системами;
5) решение краевых задач попадания из одной точки фазового пространства в другую, в частности, задача попадания в заданную область;
6) оптимальные стратегии попадания в некоторую движущуюся область.

Методы решения задач оптимального управления в основном сводятся к методу прямого поиска путем многократного нахождения процесса при вариации управляющего воздействия.

Сложность задач теории оптимального управления потребовала более широкой математической базы для ее построения. В названной теории используются вариационное исчисление, теория дифференциальных уравнений, теории матриц. Развитие оптимального управления на этой базе привело к пересмотру многих разделов теории автоматического управления, и поэтому теорию оптимального управления иногда называют современной теорией управления. Хотя это и преувеличение роли лишь одного из разделов, однако развитие теории автоматического управления определяется последние десятилетия во многом развитием этого раздела.

К настоящему времени построена математическая теория оптимального управления. На ее основе разработаны способы построения оптимальных по быстродействию систем и процедуры аналитического конструирования оптимальных регуляторов. Аналитическое конструирование регуляторов вместе с теорией оптимальных наблюдателей (оптимальных фильтров) образуют совокупность методов, которые широко используются при проектировании современных сложных систем регулирования.

Исходная информация для решения задач оптимального управления содержится в постановке задачи. Задача управления может формулироваться в содержательных (неформальных) терминах, которые часто носят несколько расплывчатый характер. Для применения математических методов необходима четкая и строгая формулировка задач, которая бы устраняла возможные неопределенности и двусмысленности и одновременно делала бы задачу математически корректной. С этой целью для общей задачи необходима адекватная ей математическая формулировка, называемая математической моделью задачи оптимизации.

Математическая модель – достаточно полное математическое описание динамической системы и процесса управления в рамках выбранной степени приближения и детализации. Математическая модель отображает исходную задачу в некоторую математическую схему, в конечном итоге – в некоторую систему чисел. В ней, с одной стороны, явно указываются (перечисляется) все сведения, без которых невозможно приступить к аналитическому или численному исследованию задачи, а с другой, – те дополнительные сведения, которые вытекают из сущности задачи и которые отражают определенное требование к ее характеристикам.

Полная математическая модель общей задачи оптимизации управления состоит из ряда частных моделей:
процесса управляемого движения;
располагаемых ресурсов и технических ограничений;
показателя качества процесса управления;
управляющих воздействий.

Таким образом, математическая модель общей задачи управления характеризуется совокупностью определенных математических соотношений между ее элементами (дифференциальных уравнений, ограничений типа равенств и неравенств, функций качества, начальных и граничных условий и т. д.). В теории оптимального регулирования устанавливаются общие условия , которым должны удовлетворять элементы математической модели для того, чтобы соответствующая математическая задача оптимизации была бы:
четко определена,
имела бы смысл, т. е. не содержала условий, приводящих к отсутствию решения.

Отметим, что формулировка задач и ее математической модели в процессе исследования не остаются неизменными, а находятся во взаимодействии друг с другом. Обычно первоначальная формулировка и ее математическая модель претерпевают значительные изменения в конце исследования. Таким образом, построение адекватной математической модели напоминает итерационный процесс, в ходе которого уточняется как постановка самой общей задачи, так и формулировка математической модели. Важно подчеркнуть, что для одной и той же задачи математическая модель может быть неединственной (разные системы координат и т. д.). Поэтому необходим поиск такого варианта математической модели, для которой решение и анализ задачи были бы наиболее просты.

В теории оптимального управления широко используются следующие математические методы:
- динамическoгo программирования;
- принцип максимума;
- вариационного исчисления;
- математическoгo программирования.

Каждый из перечисленных методов имеет свои особенности и, следовательно, свою область применения.

Метод динамического программирования обладает большими возможностями. Однако для систем высокого порядка (выше четвepтoгo) использование метода весьма затруднительно. При нeскольких переменных управления реализация метода динамического программирования на ЭВМ требует объемов памяти, иногда превышающих возможности современных машин.

Принцип максимума позволяет сравнительно легко учесть oгpaничения на управляющие воздействия, подводимые к объекту управления. Метод наиболее эффективен при синтезе систем, оптимальных по быстродействию. Однако реализация метода даже с использованием ЭВМ значительно затруднена.

Вариационное исчисление применяется при отсутствии ограничений на переменные состояния и на переменные управления. Получение численного решения на базе методов вариационногo исчисления затруднительно. Метод используется, как правило, для некоторых весьма простых случаев.

Методы математического программирования (линейного, нелинейного и др.) широко применяются для решения задач оптимальнoгo управления как в автоматических, так и в автоматизированных системах . Общая идея методов заключается в отыскании экстремума функции в пространстве многих переменных при oгpaничениях в виде системы равенств и неравенств. Методы позволяют найти численное решение широкого кpyгa задач оптимального управления. Достоинствами методов математического программирования является возможность сравнительно просто учитывать ограничения на управления и переменные состояния, а также обычно допустимые требования к объему памяти.

Метод динамического программирования Беллманаоснован на решении вариационных задач по принципу - участок оптимальной тpaeктоpии от любой ее промежуточной до конечной точки также является оптимальной тpaeктopиeй между этими точками.

Суть метода динамического программирования поясним на следующем примере. Пусть требуется перевести некоторый объект из начальной точки в конечную точку. Для этого необходимо сделать nшагов, каждый из которых имеет несколько возможных вариантов. Однако, из набора возможных вариантов на каждом шаге выбирается тот, который обладает экстремальным значением функционала. Такая процедура повторяется на каждом шаге оптимизации. В конечном итоге получаем оптимальную траекторию перехода с начального состояния в конечное при соблюдении условий оптимизации.

Пусть, например, требуется выбрать режим работы локомотива, проходящего через заданные точки, на котором достигается минимум расхода топлива или времени движения, Оптимальное решение можно найти перебором возможных вариантов на вычислительной машине, однако при больших значениях n и l, что имеет место при решении большинства реальных задач, это потребовало бы чрезвычайно большогo объема вычислений. Решение этой задачи упрощается при использовании метода динамического программирования.

Для математической формулировки задачи динамического программирования предположим, что шаги в решении задачи представляют фиксированные интервалы времени, т. е. происходит квантование по времени. Требуется найти с учетом ряда ограничений закон управления u [n], переводящий объект из точки t [о] фазового пространства в точку t[n] при условии обеспечения минимума критерия оптимальности

Благодаря такому упрощению с помощью метода динамического программирования становится возможным решение задач оптимальнoгo управления, которые не решаются путем прямой оптимизации исходного функционала классическими методами вариационного исчисления. Метод динамического программирования по существу представляет собой метод составления программы для численного решения задачи на цифровых вычислительных машинах. Лишь в простейших случаях данный метод позволяет получить аналитическое выражение искомого решения и выполнять eгo исследование. С помощью метода динамического программирования возможно решение задач не только оптимального управления, но и многошагoвых задач оптимизации из самых различных областей техники.

Метод широко применяется для исследования оптимального управления как в динамических (технических), так и в экономичеcких системах. Для реализации метода динамического программирования связи в системе между выходными переменными, управлениями и критериями оптимальности могут быть заданы как в виде аналитических зависимостей, так и в виде таблиц численных данных, экспериментальных графиков и т. п.

Принцип максимума Понтрягина можно пояснить на примере задачи о максимальном быстродействии. Пусть требуется за минимальное время перевести изображающую точку из начального положения фазового пространства в конечное положение. Для каждой точки фазового пространства существуют оптимальная фазовая траектория и соответствующее минимальное время перехода в конечную точку. Bокpyг этой точки можно по строить изохроны поверхности, являющиеся гeометрическим мeстом точек с одинаковым минимальным временем перехода в эту точку. Оптимальная по быстродействию траектория из начальной точки в конечную точку в идеальном случае должна совпадать с нормалями к изохронам (на движение вдоль изохрон затрачивается время без уменьшения отрезка времени до момента достижения конечной точки), На практике ограничения, налагаемые на координаты объекта, не всегда позволяют реализовать идеальную, оптимальную по быстродействию, траекторию. Поэтому оптимальной траекторией будет та, которая максимально, насколько это позволяют ограничения, близка к ноpмалям к изохронам. Это условие математически означает, что на протяжении всей траектории скалярное произведение вектора скорости движения изображающей точки на вектор, обратный (по направлению) градиенту времени перехода в конечную точку, должно быть максимально:

где fi, Vi - координаты соответствующих векторов.

Так как скалярное произведение двух векторов равно произведению их модулей на косинус между ними, то условием оптимальности является максимум проекции вектора скорости V на направление f. Данное условие оптимальности и есть принцип максимума Понтрягина.

Таким образом, при использовании принципа максимума вариационная задача нахождения функции u, экстремизирующей функционал H, заменяется более простой задачей определения управления u, доставляющего максимум вспомогательной функции Гaмильтона. Отсюда следует и название метода принцип максимума.

Основная сложность при применении принципа максимума состоит в том, что не известны начальные значения f (0) вспомогательной функции f, Обычно задаются произвольными начальными значениями f (0), решают совместно уравнения объекта и сопряженные уравнения и получают оптимальную траекторию, которая, как правило, проходит мимо заданной конечной точки. Методом последовательных приближений посредством задания различных начальных значений f (0) находят оптимальную траекторию, проходящую через заданную конечную точку.

Принцип максимума является необходимым и достаточным условием только для линейных объектов. Для нелинейных объектов он представляется только необходимым условием, В этом случае с eгo помощью находится суженная группа допустимых управлений, среди которых, например перебором, находится оптимальное управление, если вообще оно cyществует.

Математическое программирование. Cтpoгo линейные модели, в которых использовалась пропорциональность, линейность и аддитивность, являются далеко не адекватными многим реальным ситуациям. В действительности такие зависимости, как общие затраты , выпуск продукции и т. п., от плана производства носят нелинейный характер.

Часто применение моделей линейного программирования в ycловиях нелинейности является успешным. Поэтому необходимо определять, в каких случаях линеаризованный вариант задачи является адекватным отображением нелинейного явления.

Метод математического программирования состоит в отыскании экстремума функции многих переменных при известных ограничениях в виде системы равенств и неравенств. К числу достоинств метода математического программирования можно отнести:
сложные ограничения на переменные состояния и управления учитываются достаточно просто;
объем памяти ЭВМ может быть значительно меньше, при других методах исследования.

Если имеются сведения относительно допустимого диапазона значений переменных в оптимальном решении, то, как правило, можно построить соответствующие ограничения и получить достaточно надежное линейное приближение. В тех же случаях, когда существует широкий диапазон допустимых решений и нет сведений о характере оптимального решения, построить достаточно xoрошее линейное приближение нельзя. Значимость нелинейного программирования и eгo использование постоянно возрастают.

Часто нелинейности в моделях обусловливаются эмпирическими наблюдениями соотношений, таких как непропорциональные изменения затрат, выхода продукции, показателей качества или структур но полученные соотношения, к которым относятся постулируемые физические явления, а также выведенные математически или установленные руководством правила поведения.

Множество разнообразных обстоятельств приводит к нелинейной формулировке ограничений или целевых функций. При небольшом количестве нелинейностей или, если нелинейности не существенны, увеличение объема вычислений может быть незначительным.

Всегда необходимо проанализировать размерность и сложность модели и оценить влияние линеаризации на принимаемое решение. Часто пользуются двухэтапным подходом к решению задач: строят нелинейную модель небольшой размерности, находят область, содержащую ее оптимальное решение, а затем используют более детальную модель линейного программирования большей размерности, аппроксимация параметров которой базируется на полученном решении нелинейной модели.

Для решения задач, описываемых нелинейными моделями, не существует такого универсального метода решения, как симплекс метод решения задач линейного программирования. Какой-либо метод нелинейного программирования может окaзаться весьма эффективным для решения задач одного типа и coвершенно неприемлемым для решения других задач.

Большинство методов нелинейного программирования не вceгда обеспечивает сходимость за конечное число итераций. Heкоторые методы обеспечивают монотонное улучшение значения целевой функции при переходе от одной итерации к другой.

Задача об оптимальном быстродействии всегда является актуальной. Уменьшение времени переходных процессов следящих систем позволяет за более короткий срок отрабатывать задающие воздействия. Сокращение продолжительности переходных процессов систем управления техническими объектами, роботами, и технологическими процессами ведет к повышению производительности труда.

В линейных системах автоматического управления повышение быстродействия может быть достигнуто с помощью корректирующих устройств. Например, уменьшение влияния на переходный процесс постоянной времени апериодического звена с передаточной функцией k/(Tp + 1) возможно за счет включения последовательного дифференцирующего устройства с передаточной функцией k1 (Т1р + 1)/(Т2р + 1). Эффективными методами повышения быстродействия следящих систем являются методы подавления начальных значений медленно затухающих компонент переходного процесса систем и минимизации квадратичных интегральных оценок с помощью связей по задающему воздействию. Однако эффект улучшения переходного процесса в реальных системах зависит от степени oгpaничения координат (нелинейностей) системы, Производные от внешних воздействий, обычно значительные по величине и кратковременные по длительности, ограничиваются элементами системы и не вызывают желаемого эффекта форсировки в переходном режиме. Лучшие результаты при решении задачи повышения быстродействия автоматических систем при наличии ограничений дает управление, оптимальное по быстродействию.

Задача об оптимальном быстродействии явилась первой задачей теории оптимального управления. Она сыграла большую роль в открытии одного из основных методов теории оптимального управления принципа максимума. Эта задача, являясь частным случаем задачи оптимального управления, состоит в определении такого дoпустимого управляющего воздействия, под влиянием кoтopoгo управляемый объект (процесс) переходит из начального фазового состояния в конечное за минимальное время. Критерием оптимальности в данной задаче является время.

Необходимые условия оптимальности управления для различного типа задач оптимизации получены на основе использования аналитических непрямых методов оптимизации и образуют совокупность функциональных соотношений, которым обязательно должно удовлетворять экстремальное решение.

При выводе их сделано существенное для последующего применения предположение о существовании оптимального управления (оптимального решения). Другими словами, если оптимальное решение существует, то оно обязательно удовлетворяет приведенным (необходимым) условиям. Однако этим же необходимым условиям могут удовлетворять и другие решения, не являющиеся оптимальными (подобно тому, как необходимому условию для минимума функции одной переменной удовлетворяют, например, точки максимума и точки перегиба основной функции). Поэтому, если найденное решение удовлетворяет необходимым условиям оптимальности, то это еще не означает, что оно является оптимальным.

Использование одних только необходимых условий дает возможность в принципе найти все решения, им удовлетворяющие, и отобрать затем среди них те, которые действительно являются оптимальными. Однако практически найти все решения, удовлетворяющие необходимым условиям, чаще всего не представляется возможным в силу большой трудоемкости такого процесса. Поэтому после того как найдено какое-либо решение, удовлетворяющее необходимым условиям, целесообразно проверить, является ли оно действительно оптимальным в смысле исходной постановки задачи.

Аналитические условия, выполнимость которых на полученном решении гарантирует его оптимальность, называются достаточными условиями. Формулировка этих условий и особенно их практическая (например, вычислительная) проверка часто оказывается весьма трудоемкой задачей.

В общем случае применение необходимых условий оптимальности было бы более обоснованным, если бы для рассматриваемой задачи можно было установить факт существования или существования и единственности оптимального управления. Этот вопрос является математически весьма сложным.

Проблема существования, единственность оптимального управления состоит из двух вопросов.
1 Существование допустимого управления (т. е. управления, принадлежащего заданному классу функций), удовлетворяющего заданным ограничениям и переводящего систему из заданного начального состояния в заданное конечное состояние. Иногда граничные условия задачи выбраны так, что система – в силу ограниченности ее энергетических (финансовых, информационных) ресурсов – не в состоянии их удовлетворить. В этом случае не существует решения задачи оптимизации.
2 Существование в классе допустимых управлений оптимального управления и его единственность.

Эти вопросы в случае нелинейных систем общего вида не решены еще с достаточной для приложений полнотой. Проблема осложняется также тем обстоятельством, что из единственности оптимального управления не следует единственность управления, удовлетворяющего необходимым условиям. К тому же, обычно удовлетворяется какое-либо одно, наиболее важное необходимое условие (чаще всего – принцип максимума).

Проверка дальнейших необходимых условий бывает достаточно громоздкой. Это показывает важность любой информации о единственности управлений, удовлетворяющих необходимым условиям оптимальности, а также о конкретных свойствах таких управлений.

Необходимо предостеречь от заключений о существовании оптимального управления на основании того факта, что решается «физическая» задача. На самом деле, при применении методов теории оптимального регулирования приходится иметь дело с математической моделью. Необходимым условием адекватности описания физического процесса математическая модель как раз и является существование решения для математической модели. Поскольку при формировании математической модели вводятся различного рода упрощения, влияние которых на существование решений трудно предсказать, доказательство существования является отдельной математической проблемой.

Таким образом:
из существования оптимального управления вытекает существование, по крайней мере, одного управления, удовлетворяющего необходимым условиям оптимальности; из существования управления, удовлетворяющего необходимым условиям оптимальности, не вытекает существование оптимального управления;
из существования оптимального управления и единственности управления, удовлетворяющего необходимым условиям, вытекает единственность оптимального управления; из существования и единственности оптимального управления не следует единственность управления, удовлетворяющего необходимым условиям оптимальности.

Методы оптимизации управления рационально применить:
1) в сложных технико-экономических системах, где отыскание приемлемых решений на основе опыта затруднительно. Опыт показывает, что оптимизация малых подсистем может приводить к большим потерям в критерии качества объединенной системы. Лучше приближенно решить задачу оптимизации системы в целом (пусть в упрощенной постановке), чем точно для отдельной подсистемы;
2) в новых задачах, в которых отсутствует опыт формирования удовлетворительных характеристик процесса управления. В таких случаях формулировка оптимальной задачи часто позволяет установить качественный характер управления;
3) на возможно ранней стадии проектирования, когда имеется большая свобода выбора. После определения большого количества проектных решений системы становится недостаточно гибкой и последующая оптимизация может не дать существенного выигрыша.

При необходимости определить направление изменения управления и параметров, дающих наибольшее изменение критерия качества (определение градиента качества). Следует отметить, что для хорошо изученных и долго эксплуатируемых систем методы оптимизации могут давать небольшой выигрыш, так как найденные из опыта практические решения обычно приближаются к оптимальным.

В некоторых практических задачах наблюдается определенная «грубость» оптимальных управлений и параметров, т. е. большим локальным изменением управлений и параметров отвечают малые изменения критерия качества. Это дает иногда повод к утверждению, что на практике всегда пологие и строгие методы оптимизации не нужны.

На самом деле «грубость» управления наблюдается лишь в случаях, когда оптимальное управление соответствует стационарной точке критерия качества. В этом случае изменение управления на величину и приводит к отклонению критерия качества на величину погрешности.

В случае управлений, лежащих по границе допустимой области, указанная грубость может и не иметь место. Это свойство должно исследоваться для каждой задачи специально. Кроме того, в некоторых задачах даже небольшие улучшения критерия качества, достигаемые за счет оптимизации, могут иметь существенное значение. Сложные задачи оптимизации управления часто предъявляют чрезмерные требования к характеристикам ЭВМ, используемых при решении.

Оптимальное управление

Оптимальное управление - это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы .

Для решения задачи оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния. Математическая модель для задачи оптимального управления включает в себя: формулировку цели управления, выраженную через критерий качества управления; определение дифференциальных или разностных уравнений, описывающих возможные способы движения объекта управления; определение ограничений на используемые ресурсы в виде уравнений или неравенств .

Наиболее широко при проектировании систем управления применяются следующие методы: вариационное исчисление , принцип максимума Понтрягина и динамическое программирование Беллмана .

Иногда (например, при управлении сложными объектами, такими как доменная печь в металлургии или при анализе экономической информации) в исходных данных и знаниях об управляемом объекте при постановке задачи оптимального управления содержится неопределённая или нечёткая информация, которая не может быть обработана традиционными количественными методами. В таких случаях можно использовать алгоритмы оптимального управления на основе математической теории нечётких множеств (Нечёткое управление). Используемые понятия и знания преобразуются в нечёткую форму, определяются нечёткие правила вывода принимаемых решений, затем производится обратное преобразование нечётких принятых решений в физические управляющие переменные.

Задача оптимального управления

Сформулируем задачу оптимального управления:

здесь - вектор состояния - управление, - начальный и конечный моменты времени.

Задача оптимального управления заключается в нахождении функций состояния и управления для времени , которые минимизируют функционал.

Вариационное исчисление

Рассмотрим данную задачу оптимального управления как задачу Лагранжа вариационного исчисления . Для нахождения необходимых условий экстремума применим теорему Эйлера-Лагранжа . Функция Лагранжа имеет вид: , где - граничные условия. Лагранжиан имеет вид: , где , , - n-мерные вектора множителей Лагранжа .

Необходимые условия экстремума, согласно этой теореме, имеют вид:

Необходимые условия (3-5) составляют основу для определения оптимальных траекторий. Написав эти уравнения, получаем двухточечную граничную задачу, где часть граничных условий задана в начальный момент времени, а остальная часть - в конечный момент. Методы решения подобных задач подробно разбираются в книге

Принцип максимума Понтрягина

Необходимость в принципе максимума Понтрягина возникает в случае когда нигде в допустимом диапазоне управляющей переменной невозможно удовлетворить необходимому условию (3), а именно .

В этом случае условие (3) заменяется на условие (6):

(6)

В этом случае согласно принципу максимума Понтрягина величина оптимального управления равна величине управления на одном из концов допустимого диапазона. Уравнения Понтрягина записываются при помощи функции Гамильтона Н, определяемой соотношением . Из уравнений следует, что функция Гамильтона H связана с функцией Лагранжа L следующим образом: . Подставляя L из последнего уравнения в уравнения (3-5) получаем необходимые условия, выраженные через функцию Гамильтона:

Необходимые условия, записанные в такой форме, называются уравнениями Понтрягина. Более подробно принцип максимума Понтрягина разобран в книге .

Где применяется

Принцип максимума особенно важен в системах управления с максимальным быстродействием и минимальным расходом энергии, где применяются управления релейного типа, принимающие крайние, а не промежуточные значения на допустимом интервале управления.

История

За разработку теории оптимального управления Л.С. Понтрягину и его сотрудникам В.Г. Болтянскому , Р.В. Гамкрелидзе и Е.Ф. Мищенко в 1962 г была присуждена Ленинская премия .

Метод динамического программирования

Метод динамического программирования основан на принципе оптимальности Беллмана, который формулируется следующим образом: оптимальная стратегия управления обладает тем свойством, что каково бы ни было начальное состояние и управление в начале процесса последующие управления должны составлять оптимальную стратегию управления относительно состояния, полученного после начальной стадии процесса . Более подробно метод динамического программирования изложен в книге

Примечания

Литература

Растригин Л.А. Современные принципы управления сложными объектами. - М.: Сов. радио, 1980. - 232 с., ББК 32.815, тир. 12000 экз.
Алексеев В.М., Тихомиров В.М. , Фомин С.В. Оптимальное управление. - М.: Наука, 1979, УДК 519.6, - 223 c., тир. 24000 экз.

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое "Оптимальное управление" в других словарях:

Оптимальное управление - ОУ Управление, обеспечивающее наивыгоднейшее значение определенного критерия оптимальности (КО), характеризующего эффективность управления при заданных ограничениях. В качестве КО могут быть выбраны различные технические или экономические… … Словарь-справочник терминов нормативно-технической документации

оптимальное управление - Управление, цель которого заключается в обеспечении экстремального значения показателя качества управления. [Сборник рекомендуемых терминов. Выпуск 107. Теория управления. Академия наук СССР. Комитет научно технической терминологии. 1984 г.]… … Справочник технического переводчика

Оптимальное управление - 1. Основное понятие математической теории оптимальных процессов (принадлежащей разделу математики под тем же названием: «О.у.»); означает выбор таких управляющих параметров, которые обеспечивали бы наилучшее с точки… … Экономико-математический словарь

Позволяет при заданных условиях (часто противоречивых) достичь поставленной цели наилучшим образом, напр. за минимальное время, с наибольшим экономическим эффектом, с максимальной точностью … Большой Энциклопедический словарь

Летательным аппаратом раздел динамики полёта, посвящённый развитию и использованию методов оптимизации для определения законов управления движением летательного аппарата и его траекторий, обеспечивающих максимум или минимум выбранного критерия… … Энциклопедия техники

Раздел математики, изучающий неклассические вариационные задачи. Объекты, с которыми имеет дело техника, обычно снабжены «рулями» с их помощью человек управляет движением. Математически поведение такого объекта описывается… … Большая советская энциклопедия

Позволяет при заданных условиях (часто противоречивых) достичь поставленной цели наилучшим образом, например за минимальное время, с наибольшим экономическим эффектом, с максимальной точностью. * * * ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ … Энциклопедический словарь

В автоматической системе информация о состоянии объекта управления через измерительное устройство поступает на вход управляющего устройства. Такие системы называются системами с обратной связью или замкнутыми системами. Отсутствие этой информации в алгоритме управления говорит о том, что система разомкнута. Состояние объекта управления в любой момент времени будем описывать переменными
, которые называются координатами системы или переменными состояния. Их удобно считать координатами- мерного вектора состояния.

Измерительное устройство выдает информацию о состоянии объекта. Если на основании измерения вектора
могут быть найдены значения всех координат
вектора состояния
, то говорят, что система полностью наблюдаема.

Управляющее устройство вырабатывает управляющее воздействие
. Таких управляющих воздействий может быть несколько, они образуют- мерный управляющий вектор.

На вход управляющего устройства поступает задающее входное воздействие
. Это входное воздействие несет информацию о том, какое должно быть состояние объекта. На объект управления может действовать возмущающее воздействие
, которое представляет собой нагрузку или помеху. Измерение координаты объекта, как правило, осуществляется с некоторыми погрешностями
, которые тоже носят случайный характер.

Задачей управляющего устройства является выработка такого управляющего воздействия
, чтобы качество функционирования автоматической системы в целом было бы наилучшим в некотором смысле.

Так, например, положение летательного аппарата характеризуется шестью координатами состояния. Это
- координаты центра масс,
- углы Эйлера, определяющие ориентацию летательного аппарата относительно центра масс. Положение летательного аппарата можно изменить с помощью рулей высоты, курса, элерона и с помощью уклонения вектора силы тяги. Таким образом управляющий вектор определен следующим образом:

- угол отклонения рулей высоты

- курс

- элерон

- тяга

Вектор состояния
в этом случае определяется следующим образом:

Можно поставить задачу выбора управления, с помощью которого летательный аппарат переводится из заданного начального состояния
в заданное конечное состояние
с минимальными затратами топлива или за минимальное время.

На любой угол рулей высоты, курса, элерона существуют ограничения:

- тяга сама по себе ограничена.

Мы будем рассматривать объекты управления, которые описываются дифференциальным уравнением:

(1)

Или в векторном виде:

--мерный вектор состояния объекта

--мерный вектор управляющих воздействий

- функция правой части уравнения (1)

На вектор управления
накладывается ограничение, мы будем полагать, что его значения принадлежат некоторой замкнутой областинекоторого-мерного пространства. Это означает, что управляющая функция
в любой момент времени принадлежит области(
).