Теория массового обслуживания в маркетинге. Математическая теория массового обслуживания. Нужна помощь по изучению какой-либы темы
Методы исследования систем массового обслуживания
В качестве входного потока заявок используют следующие модели потоков: регулярный, простейший, или пуассоновский, рекуррентный (с ограниченным последействием), нестационарный. Физически наиболее простым, хотя и не самым удобным для исследования и не самым распространенным в приложениях, является регулярный входящий поток, при котором заявки поступают по одной в моменты, отстоящие друг от друга на равные промежутки времени. Самый распространенный в приложениях – простейший (пуассоновский) поток, при котором заявки в систему поступают случайно.
Рекуррентный входящий поток является естественным математическим обобщением двух предыдущих. Поток называется рекуррентным, если интервалы времени между последовательными поступлениями заявок независимы и подчинены одному и тому же закону распределения. Примером такого потока может служить поток заявок, интервалы между поступлениями которых подчинены распределению Эрланга (поток Эрланга) -го порядка:
 , .
, .
Здесь - плотность распределения Эрланга; - параметр распределения; - порядок распределения. При распределение Эрланга совпадает с экспоненциальными моментами поступления заявок потока Эрланга представляются в виде суммы независимых случайных величин, имеющих показательное распределение с параметром ![]() .
.
Все описанные потоки являются стационарными. В случае, если параметр потока – это функция времени или состояния СМО, входящий поток называется нестационарным. К нестационарным потокам прибегают, когда необходимо учесть изменение интенсивностей потоков в течение дня, месяца, при изменении длины очереди и т.п.
Дисциплина очереди позволяет описать порядок обслуживания заявок, поступающих на вход системы. Обычно рассматривают следующие виды дисциплины очереди: в порядке прибытия, случайным образом, в зависимости от приоритета (прибыл последним – обслужен первым). Обслуживание заявок в зависимости от приоритета означает, что при поступлении в систему заявок с более высоким приоритетом обслуживание заявок с более низким приоритетом прекращается.
Распределение времени обслуживания характеризует механизм обслуживания (обслуживающий прибор, канал обслуживания). Обычно интервал времени, требуемый для реализации процедуры обслуживания, принадлежит к одному из следующих типов распределений: экспоненциальному, эрланговскому, нормальному, равномерному.
5.10. Задача: Марковская модель рождения и гибели
Процессы рождения и гибели в телекоммуникациях встречаются достаточно часто. Это процесс заявок и обслуживаний, процесс, описывающий последовательность выхода на связь абонентской станции и прекращения связи, жизненный цикл той или иной технологии и др.
Условие задачи : синтезировать марковскую модель рождения и гибели. Провести анализ процесса.
Постановка задачи синтеза модели.
Для вероятностей состояний дискретной марковской цепи характерна связь между двумя условными значениями состояний и :
 ,
,  , (5.79)
, (5.79)
где - вероятности перехода.
Уравнение (5.79) справедливо также и для безусловных вероятностей состояний
 . (5.80)
. (5.80)
Рассмотрим дискретную последовательность процесс , в которой допускаются как положительные, так и отрицательные скачки. Эта последовательность называется процессом рождения и гибели и определяется следующими постулатами: 1) если в момент времени система находится в состоянии  , то вероятность перехода
, то вероятность перехода  в малом интервале времени
в малом интервале времени  равна
равна  ; 2) если в момент времени система находится в состоянии
; 2) если в момент времени система находится в состоянии  , то вероятность перехода
, то вероятность перехода  в интервале времени
в интервале времени  равна
равна  ; 3) вероятность перехода в состояние, отличное от двух соседних, есть
; 3) вероятность перехода в состояние, отличное от двух соседних, есть  ; 4) вероятность сохранения прежнего состояния равна
; 4) вероятность сохранения прежнего состояния равна  ; 5) состояние является поглощающим; если изображающая точка попала в это состояние, то процесс прекращается.
; 5) состояние является поглощающим; если изображающая точка попала в это состояние, то процесс прекращается.
Решение . На основании постулатов 1-5 записываем уравнение (5.80):
,  (5.81)
(5.81)
В рассматриваемом конкретном случае, когда состояние является поглощающим, нужно полагать  . Поэтому
. Поэтому
 . (5.82)
. (5.82)
Предполагается, что в начальный (нулевой) момент времени система находится в некотором состоянии ,  , и, следовательно, начальные условия имеют вид
, и, следовательно, начальные условия имеют вид
 (5.83)
(5.83)
В общем случае при произвольных функциях и , решение уравнений (5.81) и (5.82) оказывается затруднительным. В том частном случае, когда процесс рождения и гибели является линейным:  ,
,  ,
, ![]() ,
,  , решения при начальном условии
, решения при начальном условии  даются выражениями
даются выражениями
 , ,
, ,  (5.84)
(5.84)
где  ,
,  . (5.85)
. (5.85)
Теория массового обслуживания представляет собой область прикладной математики, использующую методы теории случайных процессов и теории вероятностей для исследования различной природы сложных систем. Теория массового обслуживания непосредственно не связана с оптимизацией. Назначение ее состоит в том, чтобы на основе результатов наблюдений за «входом» в систему предсказать ее возможности и организовать наилучшее обслуживание для конкретной ситуации и понять, как последнее отразится на стоимости системы в целом. Для систем, относящихся к системам массового обслуживания, существует определенный класс задач, решение которых позволяет ответить на актуальные для сегодняшнего времени вопросы. С какой интенсивностью должно проходить обслуживание или должен выполняться процесс при заданной интенсивности и других параметрах входящего потока требований, чтобы минимизировать очередь или задержку в подготовке документа или другого вида информации? Каковы вероятность появления задержки или очереди и ее величина? Сколько времени требование находится в очереди и каким образом минимизировать его задержку? Какова вероятность потери требования (клиента)? Какова должна быть оптимальная загрузка обслуживающих каналов? При каких параметрах системы достигаются минимальные потери прибыли? К этому перечню можно добавить еще целый ряд задач.
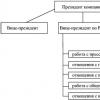
Система массового обслуживания (СМО) включает следующие структурообразующие объекты: источник требований; входной поток требований (поступление заявок); очередь; обслуживающую систему как совокупность каналов обслуживания заявок; выходной поток (об-служенные заявки или удовлетворенные требования). Рассмотрим их модели.
Источник требований. По месту нахождения источника, формиру-ющего требования, СМО делятся на разомкнутые, когда источник на-ходится вне системы, и замкнутые, когда источник находится внутри системы.?
Входной поток требований. Подавляющее большинство теоретиче-ских разработок по исследованию систем массового обслуживания вы-полнено для условия, когда входной поток требований является пуассоновским (простейшим). Этот поток обладает рядом важных свойств. Он стационарен, ординарен и не имеет последствий.
Следующее важное для исследования свойство, которым обладает пуассоновский поток, заключается в том, что процедура разделения и объединения дает снова пуассоновские потоки.
В случае разделения пуассоновского потока на N независимых по-токов получим, что интенсивность потока Х(будет равна гХ, где г.-доля /-го потока во входном потоке требований.
Очередь. Очереди, определяемые как множество требований, ожи-дающих обслуживания, представляются несколькими моделями: оче-редь с отказами, с ограниченным временем ожидания (заявка ждет определенное время), ограниченной длиной и, наконец, неограничен-ным временем ожидания. Порядок поступления заявок на обслужива-ние называется дисциплиной очереди. Требования могут принимать
ся по мере поступления, случайным порядком, с приоритетом, по принципу «последняя - первой», по определенным каналам.
Процесс обслуживания. Основным параметром процесса обслужи-вания считается время обслуживания требования каналом у - f. (/ = 1, 2,..., т). Величина тв каждом конкретном случае определяется рядом факторов: интенсивностью поступления заявок, квалификацией ис-полнителя, технологией работ, окружающей средой и т.д. Законы рас-пределения случайной величины Ту могут быть самыми различными, но наибольшее распространение в практических приложениях получил экспоненциальный закон распределения.
Важнейшее свойство экспоненциального распределения заключа-ется в следующем.
Выходной поток обслуженных требований. Выходной поток - это поток результатов деятельности, представленных выполненными тре-бованиями в виде той или иной продукции или услуги. К основным параметрам выходного потока относятся интенсивность выхода из си-стемы обслуженных требований и характер распределения времени между моментами выпуска продукции. В общем случае эти параметры определяются моделью входного потока, дисциплиной очереди и мо-делью обслуживания. Для СМО с параллельными каналами и одно-фазным обслуживанием существует теорема о том, что при пуассоновском входном потоке с параметром X и одинаковым для каждого канала распределением времени обслуживания с параметром ц в стационарном состоянии выходной поток имеет пуассоновское распределение с параметром g. В многофазных системах выходной поток одного канала служит входным потоком для другого канала.
Особенность моделей СМО связана с достаточно строгим математи-ческим описанием функционирования систем, что достигается благода-ря их унификации по ряду признаков. Так, в зависимости от модели ожидания требованием начала обслуживания различают следующие СМО:
системы с потерями или отказами;
системы с ожиданием;
системы с ограниченным временем ожидания (ВО);
системы с ограниченной длиной очереди (ДО).
По числу каналов обслуживания системы делятся на одноканальные (т = 1) и многоканальные (т > 1). Одной из форм классификации СМО служит кодовая классификация Д. Кендалла. В соответствии с этой классификацией характеристику СМО записывают в виде трех, четырех или пяти символов. Например, а/Ь/с, где а - тип распределения входного потока требований, Ъ - тип распределения времени обслуживания, с - число каналов обслуживания. Для пуассоновского и экспоненциального распределений принимают символ М, для любого произвольного распределения - символ в. Например, запись М/М/2 означает, что входной поток требований пуассоновский, время обслуживания распределено по экспоненциальному закону, в системе имеются два канала. Четвертый символ () указывает допустимую длину очереди, пятый (е) - порядок отбора требований.
Модели СМО могут быть детерминированными или вероятност-ными. В первом случае параметры и переменные модели - это посто-янные величины, во втором - случайные.
Исследование СМО заключается в нахождении показателей, харак-теризующих качество и условия работы обслуживающей системы и показателей, отражающих экономические последствия принятых ре-шений согласно первым показателям. К показателям первой группы относятся следующие.
Рассмотрим приемы вычисления показателей первой группы на
примере наиболее распространенной модели СМО (М/М/т > 2) с ожиданием, содержащей т параллельных обслуживающих каналов. Здесь поступающие требования не теряются и оставляют систему лишь после обслуживания. Каналы выполняют однородные операции, и время обслуживания каждым каналом * распределено по экспоненциальному закону с параметром т (10.5), а входящий поток - пуассоновский с параметром X (10.1); дисциплина очереди не регламентирована, и отсутствует ограничение на число поступающих требований. Модель СМО представляется в виде системы уравнений для стационарного состояния.
Пример. Требуется провести оценку эффективности централизации нескольких отделов или служб с однородными функциями. В качестве объекта рассматриваются две службы такси, которые приобрела компания «Автосервис». Заявки клиентов между службами распределяются поровну. Спрос на такси к диспетчеру поступает с частотой 10 вызовов в час. Среднее время обслуживания одного клиента составляет 11,5 мин. Вызовы такси распределены во времени по пуассоновскому закону, а продолжительность обслуживания одного клиента - по экспоненциальному закону. Каждая служба такси оснащена двумя автомобилями.
Возникает вопрос об экономической целесообразности централи-зации управления таксопарком. Для этого необходимо сравнить два варианта:
1) вариант с независимым обслуживанием системами типа (М/М/2) при51= 10 вызовов/ч,т = 11,5мин. ит = 2;
2) вариант с одной очередью типа (М/М/4) при X = 10 2 = 20 вызовов /ч, т - 11,5 мин. и /и = 4.
Приведенные оценки показывают, что централизация служб позволяет сократить среднее время ожидания клиентом вызванного по телефону такси примерно вдвое. Это не гарантия, что клиент откажется от заказа, но существенное сокращение времени ожидания. В дальнейшем, кроме создания единой службы такси, необходимо рассматривать вопросы увеличения парка такси. При решении задач с размерностью т > 5 методами теории массового обслуживания потребуется автоматизированное вычисление.
Подводя итоги, отметим, что теория массового обслуживания предоставляет исследователю множество разнообразных моделей и методов решения задач по повышению эффективности обслуживания по-
требителей, клиентов. Для ее изучения следует обратиться к фундаментальным трудам отечественных (А.Я. Хинчин, Б.В. Гнеденко, Н.П. Бусленко, И.Н. Коваленко) и зарубежных (А. Эрланг, Т.А. Саати, Г. Вагнер, X. Taxa) ученых, а также и к другим современным публикациям, например.
1. Основные понятия теории массового обслуживания.
2. Постановка задачи теории очередей.
3. Подходы решения задач теории очередей.
Краткое содержание темы
Практическая деятельность человека тесно связана с различного рода системами массового обслуживания. В области экономики - это банковское обслуживание, пользование объектами торговли и услугами сферы обслуживания и многие другие виды экономической деятельности.
Любая система массового обслуживания может включать в себя следующие элементы:
Входящий поток требований или заявок на обслуживание. Этот элемент является основным. Изучение входящего потока требований и его описание необходимо при организации любой системы массового обслуживания.
Очередь. В тех случаях, когда поступающие в систему массового обслуживания требования не могут быть удовлетворены немедленно, возникает очередь. В такой ситуации интерес может представлять длина этой очереди, порядок, по которому ожидающие требования направляются на обслуживание (как говорят, дисциплина очереди), время ожидания.
В отдельных случаях систем массового обслуживания очереди не допускаются, т.е. требование, заставшее систему занятой, не обслуживается (получает отказ).
Обслуживающее устройство. Этот элемент присутствует в любой системе массового обслуживания. От характеристик и параметров, способов организации обслуживающего устройства зависят не только время, необходимое на обслуживание одного требования, но и длина очереди и время ожидания.
Выходящий поток обслуженных требований. Этот элемент может оказаться очень важным в тех случаях, когда выходящий поток обслуженных требований является входящим для другой системы массового обслуживания.
Как правило, число требований на входе системы массового обслуживания за какой-либо промежуток времени и время обслуживания одного требования являются случайными величинами. Функционирование системы массового обслуживания в таком случае представляет собой случайный процесс, и методы исследования таких систем используют имитационное моделирование. Однако понять сущность задач и методов теории массового обслуживания можно на примерах детерминированных моделей систем массового обслуживания и прежде всего моделей теории очередей.
Основными компонентами модели очереди являются:
описание входящего потока требований;
описание способа, которым выполняется обслуживание (т.е. описание дисциплины обслуживания);
описание дисциплины очереди (т.е. каким образом из очереди выбираются клиенты на обслуживание: “первый пришел - первый обслужен”, “последний пришел - первый обслужен”, “по указанным приоритетам” и т.п.).
При конструировании модели очереди первоочередной задачей является символическое представление основных компонент, после чего изучаются соотношения между ними.
Принципиальными характеристиками очереди являются:
длина очереди в различные моменты времени;
общая продолжительность нахождения требования в системе обслуживания (т.е. время, потраченное на ожидание в очереди, плюс собственное время обслуживания);
время, в течение которого обслуживающее устройство было свободно.
Основной целью исследования систем массового обслуживания является установление равновесия между допустимыми нагрузками обслуживающего устройства, ограниченной пропускной способностью системы и раздражением клиента, с одной стороны, и допустимой стоимостью обслуживающих точек, с другой.
Рассмотрим систему массового обслуживания, имеющую один источник требований, проходящих через единственное обслуживающее устройство. Пусть имеют место следующие предположения:
1. Требования поступают через одинаковые интервалы времени. Каждый интервал имеет длину a единиц.
2. Требования обслуживаются за одинаковые интервалы времени, каждый интервал имеет длину b единиц. При этом, как только закончится обслуживание одного требования, обслуживающее устройство готово к обслуживанию следующего требования.
3. Дисциплина очереди устанавливается по правилу “Первый пришел - первый обслуживается”. Другими словами, ожидающие требования образуют очередь, и, когда обслуживающее устройство освободится, на обслуживание поступает требование, имеющее большее время ожидания.
Определим длину очереди как общее число требований, находящихся на обслуживании и ожидающих в очереди. Представим сформулированную задачу в виде следующей схемы:
Поведение системы зависит от того, как связаны между собой величины a и b. Возможны три случая: 1) b > a; 2) b = a; 3) b < a. Рассмотрим каждый из этих случаев.
1) Случай b > a. Это значит, что скорость обслуживания 1/b меньше, чем скорость поступления требований 1/a, т.е. требования обслуживаются и покидают систему медленнее, чем прибывают. Следовательно, в этом случае будет образовываться очередь и она будет постоянно возрастать.
2) Случай b = a. Если в очереди нет требований, то первое поступившее требование сразу начнет обслуживаться. Его обслуживание закончится в тот же самый момент, в который поступит на обслуживание следующее требование. Следовательно, требований, ожидающих обслуживания, не будет.
Если же первоначально имеется очередь, то ее длина будет оставаться постоянной.
3) Случай b < a. Это значит, что скорость обслуживания больше, чем скорость поступления требований. Следовательно, какое бы ни было начальное число ожидающих обслуживания требований, длина очереди будет сокращаться до 1 или 0.
Пусть в начале процесса число требований в очереди r 2 (если первоначально есть только одно требование (r = 1), то оно будет обслужено прежде, чем поступят на обслуживание следующие требования, и очередь будет пустой).
В общем случае, пусть имеем r требований, стоящих в очереди перед началом обслуживания. Тогда число требований (N), поступивших после начала процесса обслуживания до тех пор, пока сохраняется очередь, можно определить по формуле:

где обозначение [x] означает целую часть числа x. Действительно, очередь будет отсутствовать, если через обслуживающее устройство полностью пройдет N+r требований. Для этого потребуется (N+r)b единиц времени. За это время на обслуживание поступит N требований, так что к поступлению (N+1)-го требования обслуживающее устройство будет свободно и готово обслужить его сразу без всякой очереди. Но (N+1)-е требование поступит на обслуживание через (N+1)a единиц времени, при этом будет выполнено соотношение:
Докажем, что в полученном соотношении N больше правой части не более чем на 1. Действительно, первое стоящее в очереди требование будет уже обслужено, а первое вновь поступающее на обслуживание требование еще не появится в очереди (a > b). Поэтому справедливо соотношение:
aN (N+r-1)b или.
Таким образом, если к правой части соотношения добавим 1, то оно будет тождественно равно правой части соотношения. То есть прибавление 1 к правой части соотношения приводит его к соотношению - смысл неравенства меняется на противоположный. Это и требовалось доказать.
Очевидным является то, что N есть целое число. Следовательно, если от правой части в соотношении (10.2) взять целую часть и добавить к ней 1, то, исходя из предыдущих рассуждений, получим для вычисления N выражение (10.1).
Аналогичными рассуждениями и используя (10.1) можно найти, что для вычисления времени, которое необходимо для обслуживания всех ожидающих требований, справедлива формула:

В теории очередей важной функцией является функция времени ожидания обслуживания. Обозначим ее через W(t). Определим W(t) как время, которое необходимо затратить на ожидание обслуживания требования, поступившего в момент времени t (считаем, что t = 0 соответствует началу процесса обслуживания).

Определим формулу для W(t). Легко видеть, что требование, поступившее на обслуживание в момент t T-b (величина T определяется с использованием формулы (10.3)), найдет систему обслуживания пустой или только что освободившейся. Такому требованию не придется стоять в очереди. Требование, поступившее в момент времени tT-b, найдет впереди себя требований, стоящих в очереди, причем первое из них в этот же момент поступит на обслуживающее устройство. Эта величина получается следующим образом:
(начальная (число требований, обслужен- (число поступ-
очередь) - ных к моменту времени t) + лений)
Таким образом, время ожидания W(t) для рассматриваемого требования может быть выражено формулой:
Рассмотрим i-е требование в начальной очереди (0
Обобщая полученные результаты относительно функции W(t), получим для нее следующее выражение:

где i - номер i-го требования в начальной очереди; требования поступают в моменты времени a, 2a, ...; b = na (n = 1, 2, ...).
Предмет ТМО - системы массового обслуживания (СМО) и сети массового обслуживания. Под СМО понимают динамическую систему, предназначенную для эффективного обслуживания случайного потока заявок при ограниченных ресурсах системы. Обобщённая структура СМО приведена на рисунке 3.1.
Рис. 3.1. Схема СМО.
Поступающие на вход СМО однородные заявки в зависимости от порождающей причины делятся на типы, интенсивность потока заявок типа i (i=1…M) обозначено i . Совокупность заявок всех типов - входящий поток СМО.
Обслуживание заявок выполняется m каналами. Различают универсальные и специализированные каналы обслуживания. Для универсального канала типа j считается известными функции распределения F ji () длительности обслуживания заявок произвольного типа. Для специализированных каналов функции распределения длительности обслуживания каналов заявок некоторых типов являются неопределёнными, назначение этих заявок на данный канал.
В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например, потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удалённых терминалов и т.д. При этом характерным для работы таких объектов является случайное поведение заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени.
Q - схемы можно исследовать аналитически и имитационными моделями. Последнее обеспечивает большую универсальность.
Рассмотрим понятие массового обслуживания.
В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно отобразить в виде некоторого i-ого прибора обслуживания П i , состоящего из накопителя заявок, в котором может находится одновременно l i =0…L i H заявок, где L i H - ёмкость i-ого накопителя, и канала обслуживания заявок, k i .
Рис. 3.2. Схема прибора СМО
На каждый элемент прибора обслуживания П i поступают потоки событий: в накопитель H i поток заявок w i , на канал k i - поток обслуживания u i .
Потоком событий (ПС) называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Однородный ПС характеризуется только моментами поступления этих событий (вызывающими моментами) и задаётся последовательностью {t n }={0t 1 t 2 …t n …}, где t n - момент поступления n- ого события - неотрицательное вещественное число. ОПС может быть также задан в виде последовательности промежутков времени между n-ым и n-1-ым событиями { n }.
Неоднородным ПС называется последовательность {t n , f n } , где t n - вызывающие моменты; f n - набор признаков события. Например, может быть задана принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т.п.
Рассмотрим ОПС, для которого i { n }- случайные величины, независимые между собой. Тогда ПС называется потоком с ограниченным последействием.
ПС называется ординарным , если вероятность того, что на малый интервал времени t, примыкающий к моменту времени t попадает больше одного события Р 1 (t, t) пренебрежительно мала.
Если для любого интервала t событие P 0 (t, t) + P 1 (t, t) + Р 1 (t, t)=1, P 1 (t, t) - вероятность попадания на интервал t ровно одного события. Как сумма вероятностей событий, образующих полную группу и несовместных, то для ординарного потока событий P 0 (t, t) + P 1 (t, t) 1, Р 1 (t, t)=(t), где (t)- величина, порядок малости который выше, чем t, т.е. lim((t))=0 при t0.
Стационарным ПС называется поток, для которого вероятность появления того или иного числа событий на интервале времени зависит от длины этого участка и не зависит от того, где на оси времени 0 - t взят этот участок. Для ОПС справедливо 0*P 0 (t, t) + 1*P 1 (t, t)= P 1 (t, t) - среднее число событий на интервале t. Среднее число событий, наступающих на участке t в единицу времени составляет P 1 (t, t)/t. Рассмотрим предел этого выражения при t0
lim P 1 (t, t)/t=(t)*(1/един.вр.).
Если этот предел существует, то он называется интенсивностью (плотностью) ОПС. Для стандартного ПС (t)==const.
Применительно к элементарному каналу обслуживания k i можно считать что поток заявок w i W, т.е. интервалы времени между моментами появления заявок на входе k i образуют подмножество неуправляемых переменных, а поток обслуживания u i U, т.е. интервалы времени между началом и окончанием обслуживания заявки образуют подмножество управляемых переменных.
Заявки, обслуженные каналом k i и заявки, покинувшие прибор П i по различным причинам не обслуженными, образуют выходной поток y i Y.
Процесс функционирования прибора обслуживания П i можно представить как процесс изменения состояний его элементов во времени Z i (t). Переход в новое состояние для П i означает изменение кол-ва заявок, которые в нём находятся (в канале k i и накопителе H i). Т.о. вектор состояний для П i имеет вид: , где- состояния накопителя, (=0 - накопитель пуст,=1- в накопителе одна заявка…,=- накопитель занят полностью;- состояние каналаk i (=0 - канал свободен,=1 канал занят).
Q-схемы реальных объектов образуются композицией многих элементарных приборов обслуживания П i . Если k i различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы П i и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема).
Т.о. для задания Q-схемы необходимо оператор сопряжения R, отражающий взаимосвязь элементов структуры.
Связи в Q-схеме изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы. В разомкнутой выходной поток не может снова поступить на какой-либо элемент, т.е. обратная связь отсутствует.
Собственными (внутренними) параметрами Q-схемы будут являться кол-во фаз L Ф, количество каналов в каждой фазе, L kj , j=1… L Ф, количество накопителей каждой фазы L kj , k=1… L Ф, ёмкость i-ого накопителя L i H . Следует отметить, что в теории массового обслуживания в зависимости от ёмкости накопителя применяют следующую терминологию:
системы с потерями (L i H =0, накопитель отсутствует);
системы с ожиданием (L i H );
системы с ограниченной ёмкостью накопителя Н i (смешанные).
Обозначим всю совокупность собственных параметров Q-схемы как подмножество Н.
Для задания Q-схемы также необходимо описать алгоритмы её функционирования, которые определяют правила поведения заявок в различных неоднозначных ситуациях.
В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Н i и обслуживания заявок каналом k i . Неоднородность потока заявок учитывается с помощью введения класса приоритетов.
В зависимости от динамики приоритетов Q-схемы различают статические и динамические. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, т.е. они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при моделировании. Исходя из правил выбора заявок из накопитель Н i на обслуживание каналом k i можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Н, ожидает окончания обслуживания представляющей заявки каналом k i и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель, прерывает обслуживание каналом k i заявки с более низким приоритетом и сами занимает канал (при этом вытесненная из k i заявка может либо покинуть систему, либо может быть снова записана на какое-то место в Н i).
Необходимо также знать набор правил, по которым заявки покидают Н i и k i: для Н i – либо правила переполнения, либо правила ухода, связанные с истечением времени ожидания заявки в Н i ; для k i – правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале k i , т.е. правила блокировок канала. При этом различают блокировки k i по выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q‑схеме, регулирующих поток заявок в зависимости от состояний Q‑схемы. Набор возможных алгоритмов поведения заявок в Q‑схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А.
Т.о. Q‑схема,
описывающая процесс функционирования
СМО любой сложности однозначно задаётся
в виде набора множеств: Q
=
Большие резервы повышения производительности труда и снижения издержек заложены в улучшении организации предоставления услуг как производственного, так и непроизводственного назначения. Разработка и применение усредненных нормативов на работы по обслуживанию во многих случаях не дают достаточного эффекта при определении необходимого количества персонала, так как условия, в которых осуществляются эти работы, различны даже на одном предприятии. Например, использование нормативов системы планово-предупредительного ремонта для выявления необходимого количества ремонтного персонала по текущему обслуживанию не сможет обеспечить выбор оптимального варианта в связи с тем, что объем работ по ремонту зависит от многих трудноучитываемых факторов: продолжительности работы оборудования с момента его установки, состояния оборудования и его загрузки по мощности и времени, квалификации ремонтного персонала, обеспечения запасными частями и т. п. То же самое можно сказать о роли нормативов в деятельности предприятий, осуществляющих предоставление услуг населению.
Оптимальная численность обслуживающего персонала в конкретных условиях может быть определена с помощью теории массового обслуживания.
Теория массового обслуживания, как принято ее называть в нашей стране, или теория очередей, по терминологии английских и американских авторов - одна из основных составных частей исследования операций. Постановка первых вопросов теории массового обслуживания связана с исследованиями датского ученого Эрланга, работавшего в области теории проводной связи.
Характерная особенность задач массового обслуживания, возникающих в экономике и организации производства и транспорта, в области физики частиц, автоматического управления, военного дела, в работе портов и телефонных станций, учреждений бытового обслуживания и т. д., состоит в наличии обслуживающей системы (рис. 8.6), на вход которой в какие-то неизвестные заранее моменты времени поступают заявки (требования). Например, на телефонную станцию (обслуживающая система) поступают вызовы абонентов (требования), в ремонтную мастерскую - машины на ремонт. В первом случае требования удовлетворяются, т. е. после вызова происходит соединение абонентов, если линии (каналы) обслуживания свободны, если же канал занят, требование получает отказ. Во втором случае, если обслуживающие каналы (например, бригада рабочих, осуществляющих ремонт) заняты, требование становится в очередь и ждет освобождения одного из каналов.
Рис. 8.6.
Таким образом, системы массового обслуживания можно разделить на два основных типа: системы с отказами и системы с ожиданием. Обслуживание в системе с ожиданием может осуществляться в порядке поступления требований по заранее заданному закону (устанавливается приоритет для некоторых требований по отношению к другим) или в случайном порядке.
Время ожидания в очереди может быть как неограниченным, так и ограниченным, т. е. требование, «прождав» некоторое время, покидает очередь и остается необслуженным.
Каждая система массового обслуживания характеризуется пропускной способностью, определяющейся числом каналов, их производительностью и характером потока требований. Производительность канала характеризуется временем обслуживания одного требования.
Предмет теории массового обслуживания - это установление зависимости между характером потока требований, производительностью отдельного канала, числом каналов и эффективностью обслуживания.
Показателями эффективности обслуживания в зависимости от условий задачи и целей исследования могут служить различные величины и функции: средний процент отказов, среднее время простоя, среднее время ожидания, средняя длина очереди, вероятность нулевого времени ожидания и т. д.
Поток требований, поступающих на вход системы массового обслуживания, можно считать потоком случайных событий, так как моменты поступления требований заранее неизвестны. Поток событий можно изобразить последовательностью моментов их появления на оси времени. Мы будем рассматривать поток однородных событий, различающихся лишь моментами появления. Если моменты появления событий разделены одинаковыми интервалами, поток событий называется регулярным. Однако типичен для систем массового обслуживания поток требований, поступающих в случайные моменты времени.
Поток событий называется ординарным, если вероятность попадания на элементарный участок Dt двух или более событий есть величина бесконечно малая по сравнению с вероятностью попадания одного события на этот участок. Это означает, что совпадение двух или более событий невозможно, требования приходят по одному, а не парами, тройками и т. д.
Поток событий называется стационарным, если вероятность попадания какого-то количества событий на определенный участок времени зависит только от длины этого участка, а не от расположения на оси времени, для стационарного потока характерна независимость вероятностных характеристик от времени, он имеет постоянную плотность (среднее число требований в единицу времени).
Поток событий называется потоком без последствия, если для любых неперекрывающихся участков времени количество событий, попадающих на один из них, не зависит от количества событий, попадающих на другие. Это означает, что требования поступают в систему независимо друг от друга.
Ординарный стационарный поток без последствия называется простейшим (или стационарным пуассоновским). Термин «пуассоновский поток» употребляется потому, что, как известно из теории вероятностей, для ординарного потока без последствия число событий, попадающих на участок t, распределено по закону Пуассона:

где Хх = а - математическое ожидание количества событий на участке т; X - параметр, характеризующий плотность потока (к > 0);
Рщ СО - вероятность того, что за время X произойдет т событий.
В частности, при т = 0
и есть вероятность того, что за время т не произойдет ни одного события. Отсюда можно получить
т. е. вероятность того, что за время т произойдет хотя бы одно событие.
В общем случае время обслуживания есть случайная величина, поэтому для получения количественных характеристик системы массового обслуживания необходимо задавать закон распределения времени обслуживания.
Задачи теории массового обслуживания имеют простое аналитическое решение, если поток требований является пуассоновским, а время обслуживания распределено по показательному закону:

t o6 - среднее время обслуживания требования.
В реальных задачах могут встретиться потоки более общего вида, где время обслуживания распределено не только по показательному закону.
Кроме того, различные системы массового обслуживания могут образовывать сеть, когда требования, выходящие из одних систем массового обслуживания с различными вероятностями, поступают на входы других систем или уходят из сети.
В сложных экономических системах ожидание требования начала обслуживания часто вызывает простой какой-то системы, в которую это требование должно поступить после обслуживания первой системой. В ряде случаев очень большие расходы вызывает простой обслуживающей системы (например, вычислительный центр, крупный завод), в других случаях нежелательно ожидание (например, в случае поступления очень важного заказа, важности результата для других систем и т. д.).
Обычно при решении экономических задач нужно достичь экстремального (минимального или максимального) значения некоторого критерия (функции стоимости), определяемого для различных конкретных условий. При исследовании работы систем массового обслуживания чаще всего минимизируются расходы из-за простоя и ожидания, потери вследствие ухода требования, оценивается целесообразность увеличения числа каналов.
Например, необходимо организовать ремонтное обслуживание оборудования в каком-либо цехе или на участке. Для этого нужно выделить определенное количество рабочих-ремонтников. Если рабочих будет мало, это вызовет простой оборудования в ожидании ремонта и соответственно простой производственных рабочих. Если же ремонтников будет слишком много, это приведет к нерациональному использованию их рабочего времени, к излишним затратам на их содержание. И в том и в другом случае производство будет иметь потери, которые в конечном счете обусловят снижение производительности труда и повышение себестоимости продукции. Необходимо выбрать вариант, при котором суммарные потери будут наименьшими.
Математические методы теории массового обслуживания дают возможность установить среднее количество требований, находящихся в системе, в очереди, среднее количество необслуженных требований, среднее время ожидания, вероятность отказа, вероятность того, что длина очереди не превысит заданную, и т. д.
Кратко рассмотрим подход к решению одной из классических задач теории массового обслуживания. Пусть имеется п станков и бригада из т человек, обслуживающая эти станки. Станок, работающий в момент времени t, отказывает к моменту t + т с вероятностью Р(т) = - 1 - е~ кх, где е~ кХ есть вероятность того, что за время t не произойдет ни одного отказа. Время ремонта станка - случайная величина г). Для такой системы можно вычислить среднее число простаивающих рабочих. Эта характеристика используется в дальнейшем для оптимального выбора соотношения между пит исходя из экономических критериев.
С применением методов теории массового обслуживания можно решать также задачи выбора наиболее рациональной организации многостаночного обслуживания. Например, необходимо установить, какое количество автоматов может эффективно обслуживать один рабочий. Если у рабочего будет слишком много станков, то неизбежны простои оборудования из-за того, что он не будет успевать своевременно заправлять их материалом, проверять качество изготовленной детали и т. п., если же обслуживаемых станков будет мало, рабочий будет систематически простаивать.
Задача в данном случае состоит в том, чтобы выбрать, исходя из конкретных условий работы оборудования и рабочего, наиболее выгодный для производства вариант.
Методы теории массового обслуживания смогут использоваться и при решении такого типа задач, как определение оптимальной численности бригады, обслуживающей какие-либо агрегаты (вагранки, печи и т. д.), определение необходимого количества транспортных средств для нужд цехов и т. д.
Рассмотрим математический аппарат, с помощью которого можно оценить функционирование в стационарном режиме простейших систем массового обслуживания с отказами при условии поступления в них пуассоновского потока требований. Такая задача впервые была решена Эрлангом, который получил следующие зависимости :
Вероятность того, что обслуживанием заняты К аппаратов (линий, приборов и т. д.)

где А - плотность потока заявок;
п - число аппаратов (линий, приборов и т. д.); т - параметр обслуживания.
Чаще всего в формулах используется параметр а = А/p, тогда предыдущую формулу запишем так:

Частными случаями этой формулы будут:
Вероятность того, что все обслуживающие аппараты свободны:

Вероятность того, что все обслуживающие аппараты заняты. Это одновременно и вероятность отказа в обслуживании вновь поступившего требования в систему:

На практике необходимо часто определять:
Среднее число приборов, занятых обслуживанием, и связанный с ними коэффициент занятости аппаратов:
Это будет и доля загруженных аппаратов за время обслуживания:
Среднее число аппаратов, свободных от обслуживания:
Коэффициент простоя аппаратов:
При решении практических задач целесообразно для проверки правильности полученных результатов пользоваться вполне очевидным равенством
Было доказано, что формулы Эрланга справедливы не только для случая, когда время распределено по показательному закону, но и для случаев любого распределения времени обслуживания. Этот результат позволит значительно расширить области применения формул Эрланга для решения многих практических задач.
Рассмотрим несколько примеров.
Пример 1. Необходимо оценить работу автоматизированной телефонной станции (АТС), которая имеет п = 5 линий связи. К услугам станции обращаются абоненты с требованиями на ведение разговоров. Естественно, что моменты поступления требований на станцию случайны и независимы друг от друга.
Задачу решим на примере простейшего потока требований. Пусть средняя плотность потока вызовов в единицу времени X = 2. Продолжительность каждого разговора - также величина случайная. Можно принять, что продолжительность разговоров различных абонентов подчинена показательному закону распределения. Пусть среднее время, необходимое для ведения каждого разговора, равно t o6 = 1 ед. времени. Может возникнуть сомнение в правомочности принятия показательного закона распределения времени ведения разговоров абонентов. Но, как уже говорилось выше, формулами Эрланга можно пользоваться при любых законах распределения времени разговоров абонентов.
В итоге в предлагаемом примере необходимо оценить функционирование АТС.
Решение
Находим параметр
Вероятность того, что все линии будут свободны при работе АТС, может быть определена по формуле (8.24):

Вероятность того, что абоненту будет отказано в обслуживании, рассчитывается по формуле (8.25):

Определяем среднее число занятых линий связи во время работы АТС.
Для проведения необходимых расчетов составим таблицу 8.3.
Таблица для расчета параметров задачи
По результатам расчетов получено:
Коэффициент простоя линий равен:

При решении этого примера целесообразно воспользоваться специальной таблицей 4 приложения 5 к книге (подобные таблицы приводятся и в других работах по массовому обслуживанию). Входом в нее является К и а, а из таблицы можно получить значения вероятностей Р к и их частных значений Р 0 и Р п.
Пример 2. Необходимо спроектировать АТС с пропускной способностью, при которой вероятность получения абонентом отказа в обслуживании не превосходила Р п X = 0,5 вызова в минуту. Считается, что средняя продолжительность разговора равна f o6 -2 мин. Определить необходимое число линий связи.
Значит, коэффициент загрузки линий связи равен:

Среднее число свободных линий связи равно:
Решение
Определяем параметр
Для составления расчетной таблицы воспользуемся таблицей 4 приложения 5 к работе .
Таблица 8.4
Определение вероятностей
Из данных таблицы 8.4 следует, что АТС нужно проектировать на 5 линий связи. При этом будет обеспечена связь одного абонента с другими с вероятностью Р = 0,997.
Несмотря на достаточно обширную область возможного применения теории массового обслуживания, следует отметить, что часто бывает довольно трудно подобрать подходящую модель для описания конкретной ситуации, а когда это удается, то возникают алгоритмические трудности ее решения.
- Вывод приводимых ниже формул можно найти в работе .