Абстрактное бинарное дерево

Лекция Деревья

Деревья (trees) используются для представления отношения. Все деревья являются иерархическими по своей сути. Интуитивное значение этого термина состоит в том, что между узлами дерева существует отношение "родительский-дочерний". Если ребро со­единяет узел n и узел т, причем узел п находится выше узла т, то узел n счи­тается родителем (parent) узла т, а узел т - его дочерним узлом (child) . В де­реве, изображенном на рис. 10.1, узлы В и С являются дочерними по отношению к узлу А. Дочерние узлы, имеющие одного и того же родителя, - например, уз­лы В и С - называются братьями (siblings) . Каждый узел дерева имеет по крайней мере одного родителя, причем в дереве существует только один узел, не имеющий предков. Такой узел называется корнем дерева (root) . На рис. 10.1 корнем является узел А. Узел, у которого нет дочерних узлов, называется лис­том дерева (leaf). Листьями дерева, изображенного на рис. 10.1, являются узлы С, D, Е и F.

Рис. 10.1. Дерево общего в

Отношения между родительским и дочерним узлом с абстрактной точки зре­ния является отношением между предком (ancestor) и потомком (descendant). На рис. 10.1 узел А является предком узла Д следовательно, узел D является по­томком узла А. Не все узлы могут быть связаны отношениями "предок-потомок": узлы В и С, например, не связаны родственными отношениями. Однако корень любого дерева является предком каждого его узла. Поддеревом (subtree) называется любой узел дерева со всеми его потомками. Поддеревом узла п является поддерево, корнем которого является узел n. Например, на рис. 10.2 показано поддерево дерева, изображенного на рис. 10.1. Корнем этого поддерева является узел В, а само поддерево является поддеревом узла А.

С формальной точки зрения, дерево общего вида (general tree) T представляет собой множество, состоящее из одного или нескольких узлов, принадлежащих непересекающимся подмножествам, указанным ниже.

Отдельный узел r, корень.

Множество поддеревьев корня r.

Бинарное дерево (binary tree) - это множество узлов Т, таких что

Множество Т пусто, или

Множество Т распадается на три непересекающихся подмножества:

Отдельный корень r, корень;

Два возможно пустых поддерева бинарного дерева, которые называются левым и правым поддеревьями (leaf and right subtrees) корня r, соответственно.

В качестве иллюстрации использования бинарных деревьев для представле­ния данных в иерархическом виде рассмотрим рис. 10.4. На этом рисунке би­нарные деревья представляют алгебраические выражения, содержащие бинарные операторы +, -, * и /. Для представления выражения а-b оператор помещается в корневой узел, а операнды а и b- в его левый и правый дочерние узлы, соответственно (рис. 10.4). На рис. 10.4, б представлено выражение a-b/с, где поддерево представляет подвыражение b/с. Аналогичная ситуация показана на рис. 10.4, в, где изображено выражение (а-b)*с. В узлах этих деревьев хранятся операнды выражений, а в остальных узлах - операторы. Скобки в этих деревьях не представлены. Бинарное дерево создает иерархию операций, т.е. дерево однозначно определяет порядок вычисления выражения.

Рис. 10.4. Бинарные деревья, представляющие алгебраические выражения

Бинарное дерево поиска - это бинарное дерево, некоторым образом упорядоченное в соответ­ствии со значениями, содержащимися в его узлах. Каждый узел п бинарного де­рева поиска обладает следующими тремя свойствами:

Значение узла п больше всех значений, содержащихся в левом поддереве TL.

Значение узла п меньше всех значений, содержащихся в правом поддереве ТR.

Деревья TL и ТR являются деревьями бинарного поиска.

На рис. 10.5 показан пример бинарного дерева поиска. Как следует из его назва­ния, это дерево обеспечивает возможности поиска конкретного элемента. Позд­нее мы рассмотрим эту структуру данных более подробно.

Высота деревьев. Деревья могут иметь разную форму. Например, хотя деревья, изображенные на рис. 10.6, состоят из одинаковых узлов, они имеют совершенно разную структуру. Каждое из этих деревьев содержит семь узлов, но некоторые деревья "выше" других. Высота (height) дерева - это количество узлов, располо­женных на самом длинном пути от корня к листу. Например, высота деревьев, по­казанных на рис. 10.6, равна 3, 5 и 7, соответственно. Интуитивное представление о высоте деревьев может привести к заключению, что их высота равна 2, 4 и 6, соответственно. Действительно, многие авторы используют именно интуитивное оп­ределение высоты дерева (подсчитывая количество ребер на самом длинном пути от корня до дерева. - Прим. ред.). Однако принятое нами определение позволяет более четко формулировать многие алгоритмы и свойства деревьев.

Полное, совершенное и сбалансированное дерево. В полном бинарном дереве(full binary tree), имеющем высоту h, все узлы, расположенные на уровнях, меньших уровня h, имеют по два дочерних узла. На рис. 10.7 представлено пол­ное бинарное дерево, имеющее высоту, равную 3. Каждый узел полного бинарно­го дерева имеет левое и правое поддерево, имеющие одинаковую высоту . Среди всех бинарных деревьев, высота которых равна h, полное бинарное дерево имеет максимально возможное количество листьев, и все они расположены на уровне h. Проще говоря, в полном бинарном дереве нет пропущенных узлов.

Доказывая свойства полных бинарных деревьев, подсчитывая количество их узлов, удобно пользоваться рекурсивным определением.

Если дерево Т пусто, то оно является полным бинарным деревом, имеющим

высоту, равную 0.

Если дерево T не пусто, и его высота равна h > 0, то дерево T является полным бинарным деревом, если поддеревья его корня являются полными бинарными деревьями, имеющими высоту h-1.

Это определение хорошо отражает рекурсивную природу бинарного дерева.

Совершенное бинарное дерево (complete binary tree), имеющее высоту h, - это бинарное дерево, которое является полным вплоть до уровня h-1, а уровень h заполнен слева направо так, как показано на рис. 10.8.

Рис. 10.8. Совершенное бинарное дерево

Очевидно, что полное бинарное дерево является совершенным.

Бинарное дерево называется сбалансированным по высоте (height balanced), или просто сбалансированным (balanced), если высота правого поддерева любого его узла отличается от высоты левого поддерева не больше, чем на 1. Бинарные деревья, изображенные на рис. 10.8 и 10.6, а, яв­ляются сбалансированными, а деревья, представленные на рис. 10.6, б и 10.6, в - нет. Совершенное бинарное дерево является сбалансированным. Итак, повторим кратко введенные понятия.

Абстрактное бинарное дерево

B бинарном дереве существует несколько способов обхода. Стандартными являются три порядка обхода дерева: прямой, симметричный и обратный. Все они описываются в следующем разделе. Над абстрактным бинарным деревом выполняются следующие операции.

Деревья являются одними из наиболее широко распространенных структур данных в информатике и программировании, которые представляют собой иерархические структуры в виде набора связанных узлов.

– это структура данных , представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов ( рис. 31.1). Каждый элемент дерева называется вершиной (узлом) дерева . Вершины дерева соединены направленными дугами, которые называют ветвями дерева . Начальный узел дерева называют корнем дерева , ему соответствует нулевой уровень. Листьями дерева называют вершины, в которые входит одна ветвь и не выходит ни одной ветви.

Каждое дерево обладает следующими свойствами:

1. существует узел, в который не входит ни одной дуги (корень);
2. в каждую вершину, кроме корня, входит одна дуга.

Деревья особенно часто используют на практике при изображении различных иерархий. Например, популярны генеалогические деревья.

Рис. 31.1.

Все вершины, в которые входят ветви, исходящие из одной общей вершины, называются потомками , а сама вершина – предком . Для каждого предка может быть выделено несколько. Уровень потомка на единицу превосходит уровень его предка. Корень дерева не имеет предка, а листья дерева не имеют потомков.

Высота (глубина) дерева определяется количеством уровней, на которых располагаются его вершины. Высота пустого дерева равна нулю, высота дерева из одного корня – единице. На первом уровне дерева может быть только одна вершина – корень дерева , на втором – потомки корня дерева, на третьем – потомки потомков корня дерева и т.д.

Поддерево – часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева.

Степенью вершины в дереве называется количество дуг, которое из нее выходит. Степень дерева равна максимальной степени вершины, входящей в дерево . При этом листьями в дереве являются вершины, имеющие степень нуль. По величине степени дерева различают два типа деревьев:

• двоичные – степень дерева не более двух;
• сильноветвящиеся – степень дерева произвольная.

Упорядоченное дерево – это дерево , у которого ветви, исходящие из каждой вершины, упорядочены по определенному критерию.

Деревья являются рекурсивными структурами, так как каждое поддерево также является деревом. Таким образом, дерево можно определить как рекурсивную структуру, в которой каждый элемент является:

• либо пустой структурой;
• либо элементом, с которым связано конечное число поддеревьев.

Действия с рекурсивными структурами удобнее всего описываются с помощью рекурсивных алгоритмов.

Списочное представление деревьев основано на элементах, соответствующих вершинам дерева. Каждый элемент имеет поле данных и два поля указателей: указатель на начало списка потомков вершины и указатель на следующий элемент в списке потомков текущего уровня. При таком способе представления дерева обязательно следует сохранять указатель на вершину, являющуюся корнем дерева .

Для того, чтобы выполнить определенную операцию над всеми вершинами дерева необходимо все его вершины просмотреть. Такая задача называется обходом дерева .

Обход дерева – это упорядоченная последовательность вершин дерева, в которой каждая вершина встречается только один раз.

При обходе все вершины дерева должны посещаться в определенном порядке. Существует несколько способов обхода всех вершин дерева. Выделим три наиболее часто используемых способа обхода дерева ( рис. 31.2):

• прямой;
• симметричный;
• обратный.

Существует большое многообразие древовидных структур данных. Выделим самые распространенные из них: бинарные (двоичные) деревья, красно-черные деревья, В-деревья, АВЛ-деревья , матричные деревья, смешанные деревья и т.д.

Бинарные деревья

Бинарные деревья являются деревьями со степенью не более двух.

Бинарное (двоичное) дерево – это динамическая структура данных , представляющее собой дерево , в котором каждая вершина имеет не более двух потомков ( рис. 31.3). Таким образом, бинарное дерево состоит из элементов, каждый из которых содержит информационное поле и не более двух ссылок на различные бинарные поддеревья. На каждый элемент дерева имеется ровно одна ссылка .

Каждая вершина бинарного дерева является структурой, состоящей из четырех видов полей. Содержимым этих полей будут соответственно:

• информационное поле (ключ вершины);
• служебное поле (их может быть несколько или ни одного);
• указатель на левое поддерево ;
• указатель на правое поддерево .

По степени вершин бинарные деревья делятся на ( рис. 31.4):

• строгие – вершины дерева имеют степень ноль (у листьев) или два (у узлов);
• нестрогие – вершины дерева имеют степень ноль (у листьев), один или два (у узлов).

Двоичное дерево – вид связного ациклического (не имеющего циклов) графа, характерный тем, что у каждого из его узлов имеется не более двух потомков (связанных узлов, находящихся иерархически ниже).

Определения следующего абзаца не относятся непосредственно к двоичным деревьям, а скорее к вообще, поэтому тем, у кого не возникает проблем с понятиями можно перейти к следующему абзацу.

В двоичном дереве есть только один узел, у которого нет предка, он называется корнем . Конечные узлы – листья . Если у корня отсутствует предок, то у листьев – потомки. Все вершины помимо корня и листьев называются узлами ветвления . Длина пути от корня до узла определяет уровень этого самого узла. Уровень корня дерева всегда равен нулю, а уровень всех его потомков определяется удаленностью от него. Например, узлы F и L (рис. ниже) расположены на первом уровне, а U и B – на третьем.

Связный граф является деревом тогда и только тогда, когда P - A =1 , где P – количество вершин в графе, а A – количество ребер, поскольку в любом дереве с n вершинами, должно быть n -1 ребро. Это справедливо и для бинарного дерева, так как оно входит в класс деревьев. А увидеть отличительные признаки бинарного дерева , можно просто зная его определение. Достаточно взглянуть на рисунок 1, чтобы понять является ли изображенный на нем граф бинарным деревом.

Во-первых, он связный и не имеет ни одного цикла (следовательно, имеем дело с деревом), во-вторых из каждого узла исходит не больше двух ребер (если бы граф был неориентированным, то допускалось три исходящих ребра), что указывает на главный признак двоичного дерева. Но существует и немного другой способ проверить является ли дерево бинарным. Составим список, в левом столбце которого будут содержаться номера уровней, а в правом – число вершин, лежащих на каждом из них:

Обозначим уровень символом k , а количество вершин n , тогда для бинарного дерева будет справедливо равенство n ≤ 2 k , т. е. количество вершин на k -ом уровне не может иметь значение большее, чем степень двойки этого уровня. Для доказательства этого достаточно построить полное дерево, все уровни которого содержат максимально возможное для двоичного дерева количество вершин: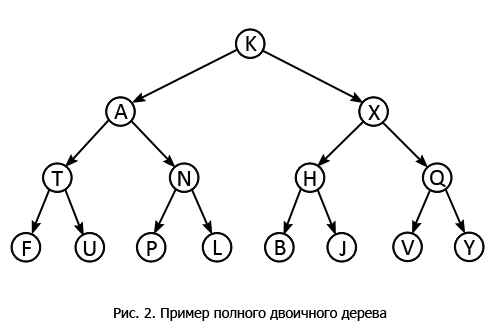

Продолжая построение, будем получать на каждом новом уровне число вершин равное k -ой степени двойки, а их общее количество вычисляется по формуле:Для рисунка 2 формула раскрывается так: 2 0 +2 1 +2 2 +2 3 =15.

Операция, при которой вершины дерева поочередно просматриваются и каждая только один раз, называется обходом дерева . Выделяют четыре основных метода обхода:

• обход в ширину;
• прямой обход;
• обратный обход;
• симметричный обход;

Обход в ширину – это поуровневая обработка узлов слева на право. Работа метода заключается в просмотре всех вершин, начиная с некоторой вершины на n-ом уровне.

Возьмем нулевой уровень за начальный (рис. 2), и, начиная с вершины K , будем методом обхода в ширину поочередно двигаться вниз, просматривая вершины в следующем порядке: K A X T N H Q F U P L B J V Y.

Обход в прямом порядке вначале предполагает обработку узлов предков, а потом их потомков, то есть сначала посещается вершина дерева, далее левое и правое поддеревья, именно в описанном порядке. Для нашего дерева последовательность прямого обхода такая: K A T F U N P L X H B J Q V Y.

Обход в обратном порядке противоположен прямому обходу. Первыми осматриваются потомки, а уже затем предки, иначе говоря, первоначально обращение идет к элементам нижних уровней левого поддерева, потом то же самое с элементами правого, и в конце осматривается корень. Обратный обход дерева с рисунка 2: F U T P L N A B J H V Y Q X K.

Обход в симметричном порядке заключается в посещении левого узла, перехода в корень и оттуда в правый узел. Все для того же дерева узлы будут осмотрены в следующем порядке: F T U A P N L K B H J X V Q Y.

На практике используются не просто бинарные деревья, а их частные случаи, например, такие как двоичное дерево поиска, АВЛ-дерево, двоичная куча и другие.

Теги: Двоичное дерево поиска. БДП. Итреативные алгоритмы работы с двоичным деревом поиска.

Двоичное дерево поиска. Итеративная реализация.

Д воичные деревья – это структуры данных, состоящие из узлов, которые хранят значение, а также ссылку на свою левую и правую ветвь. Каждая ветвь, в свою очередь, является деревом. Узел, который находится в самой вершине дерева принято называть корнем (root), узлы, находящиеся в самом низу дерева и не имеющие потомков называют листьями (leaves). Ветви узла называют потомками (descendants). По отношению к своим потомкам узел является родителем (parent) или предком (ancestor). Также, развивая аналогию, имеются сестринские узлы (siblings – родные братья или сёстры) – узлы с общим родителем. Аналогично, у узла могут быть дяди (uncle nodes) и дедушки и бабушки (grandparent nodes). Такие названия помогают понимать различные алгоритмы.

Двоичное дерево. На этом рисунке узел 10 корень, 7 и 12 его наследники. 6, 9, 11, 14 - листья. 7 и 12, также как и 6 и 9 являются сестринскими узлами, 10 - это дедушка узла 6, а 12 - дядя узла 6 и узла 9

Двоичные деревья одна из самых простых структур (по сравнению, например, с другими деревьями). Они обычно реализуют самый базовый и самый естественный способ классификации элементов – делят их по определённому признаку, размещая одну группу в левом поддереве, а другую группу в правом. В поддеревьях рекурсивно поддерживается такой же порядок, за счёт чего узлы дерева упорядочиваются.

Такое размещение – слева меньше, справа больше – не обязательно, можно располагать элементы, которые меньше, справа. Отношение БОЛЬШЕ и МЕНЬШЕ – это не обязательно естественная сортировка по величине, это некоторая бинарная операция, которая позволяет разбить элементы на две группы.

Для реализации бинарного дерева поиска будем использовать структуру Node, которая содержит значение, ссылку на правое и левое поддерево, а также ссылку на родителя. Ссылка на родительский узел, в принципе, не является обязательной, однако сильно упрощает и ускоряет все алгоритмы. Далее, ради тренировки, мы ещё рассмотрим реализацию без ссылки на родителя.

ЗАМЕЧАНИЕ: мы рассматриваем случай, когда в дереве все значения разные и не равны NULL. Деревья с повторяющимися узлами рассмотрим позднее.

Обычно в качестве типа данных мы используем void* и далее передаём функции сравнения через указатели. В этот раз будем использовать пользовательский тип и макросы.

Typedef int T; #define CMP_EQ(a, b) ((a) == (b)) #define CMP_LT(a, b) ((a) < (b)) #define CMP_GT(a, b) ((a) > (b)) typedef struct Node { T data; struct Node *left; struct Node *right; struct Node *parent; } Node;

Сначала, как обычно, напишем функцию, которая создаёт новый узел. Она принимает в качестве аргументов значение и указатель на своего родителя. Корневой элемент не имеет родителя, значение указателя parent равно NULL.

Node* getFreeNode(T value, Node *parent) { Node* tmp = (Node*) malloc(sizeof(Node)); tmp->left = tmp->right = NULL; tmp->data = value; tmp->parent = parent; return tmp; }

Разберёмся со вставкой. Возможны следующие ситуации

• 1) Дерево пустое. В этом случае новый узел становится корнем ДДП.
• 2) Новое значение меньше корневого. В этом случае значение должно быть вставлено слева. Если слева уже стоит элемент, то повторяем эту же операцию, только в качестве корневого узла рассматриваем левый узел. Если слева нет элемента, то добавляем новый узел.
• 3) Новое значение больше корневого. В этом случае новое значение должно быть вставлено справа. Если справа уже стоит элемент, то повторяем операцию, только в качестве корневого рассматриваем правый узел. Если справа узла нет, то вставляем новый узел.

Пусть нам необходимо поместить в ДДП следующие значения

10 7 9 12 6 14 11 3 4

Первое значение становится корнем.

Дерево с одним узлом. Равных NULL потомков не рисуем

Второе значение меньше десяти, так что оно помещается слева.

Если значение меньше, то помещаем его слева

Число 9 меньше 10, так что узел должен располагаться слева, но слева уже стоит значение. 9 больше 7, так что новый узел становится правым потомком семи.

Двоичное дерево поиска после добавления узлов 10, 7, 9

Число 12 помещается справа от 10.

6 меньше 10 и меньше 7...

Добавляем оставшиеся узлы 14, 3, 4, 11

Функция, добавляющая узел в дерево

Два узла. Первый – вспомогательная переменная, чтобы уменьшить писанину, второй – тот узел, который будем вставлять.

Node *tmp = NULL; Node *ins = NULL;

Проверяем, если дерево пустое, то вставляем корень

If (*head == NULL) { *head = getFreeNode(value, NULL); return; }

Проходим по дереву и ищем место для вставки

Tmp = *head;

Пока не дошли до пустого узла

While (tmp) {

Если значение больше, чем значение текущего узла

If (CMP_GT(value, tmp->data)) {

Если при этом правый узел не пустой, то за корень теперь считаем правую ветвь и начинаем цикл сначала

If (tmp->right) { tmp = tmp->right; continue;

Если правой ветви нет, то вставляем узел справа

} else { tmp->right = getFreeNode(value, tmp); return; }

Также обрабатываем левую ветвь

} else if (CMP_LT(value, tmp->data)) { if (tmp->left) { tmp = tmp->left; continue; } else { tmp->left = getFreeNode(value, tmp); return; } } else { exit(2); } }

Void insert(Node **head, int value) { Node *tmp = NULL; Node *ins = NULL; if (*head == NULL) { *head = getFreeNode(value, NULL); return; } tmp = *head; while (tmp) { if (CMP_GT(value, tmp->data)) { if (tmp->right) { tmp = tmp->right; continue; } else { tmp->right = getFreeNode(value, tmp); return; } } else if (CMP_LT(value, tmp->data)) { if (tmp->left) { tmp = tmp->left; continue; } else { tmp->left = getFreeNode(value, tmp); return; } } else { exit(2); } } }

Рассмотрим результат вставки узлов в дерево. Очевидно, что структура дерева будет зависеть от порядка вставки элементов. Иными словами, форма дерева зависит от порядка вставки элементов.

Если элементы не упорядочены и их значения распределены равномерно, то дерево будет достаточно сбалансированным, то есть путь от вершины до всех листьев будет одинаковый. В таком случае максимальное время доступа до листа равно log(n), где n – это число узлов, то есть равно высоте дерева.

Но это только в самом благоприятном случае. Если же элементы упорядочены, то дерево не будет сбалансировано и растянется в одну сторону, как список; тогда время доступа до последнего узла будет порядка n. Это слабая сторона ДДП, из-за чего применение этой структуры ограничено.

Дерево, которое получили вставкой чередующихся возрастающей и убывающей последовательностей (слева) и полученное при вставке упорядоченной последовательности (справа)

Для решения этой проблемы можно производить балансировку дерева, или использовать структуры, которые автоматически проводят самобалансировку во время вставки и удаления.

Поиск в дереве

И звестно, что слева от узла располагается элемент, который меньше чем текущий узел. Из чего следует, что если у узла нет левого наследника, то он является минимумом в дереве. Таким образом, можно найти минимальный элемент дерева

Node* getMinNode(Node *root) { while (root->left) { root = root->left; } return root; }

Аналогично, можно найти максимальный элемент

Node* getMaxNode(Node *root) { while (root->right) { root = root->right; } return root; }

Опять же, если дерево хорошо сбалансировано, то поиск минимума и максимума будет иметь сложность порядка log(n), а в случае плохой балансировки стремится к n.

Поиск нужного узла по значению похож на алгоритм бинарного поиска в отсортированном массиве. Если значения больше узла, то продолжаем поиск в правом поддереве, если меньше, то продолжаем в левом. Если узлов уже нет, то элемент не содержится в дереве.

Node *getNodeByValue(Node *root, T value) { while (root) { if (CMP_GT(root->data, value)) { root = root->left; continue; } else if (CMP_LT(root->data, value)) { root = root->right; continue; } else { return root; } } return NULL; }

Удаление узла

С уществует три возможных ситуации.

• 1) У узла нет наследников (удаляем лист). Тогда он просто удаляется, а его родитель обнуляет указатель на него.

  Удаляем лист

  Просто исключаем его из дерева

• 2) У узла один наследник. В этом случае узел подменяется своим наследником.

У узла 6 один наследник

Копируем на его место единственного наследника

• 3) У узла оба наследника. В этом случае узел не удаляем, а заменяем его значение на максимум левого поддерева. После этого удаляем максимум левого поддерева. (Напомню, что мы условились, что слева элементы меньше корневого).

  У узла 7 два наследника. Находим максимум его левого поддерева (это 6)

  Узел не удаляем, а копируем на его место значение максимума левого поддерева и удаляем этот узел

Максимум левого поддерева имеет не более одного наследника, так что он удаляется просто. Известно, что все значения слева от корня меньше корня. Соответственно, максимум левого поддерева будет, с одной стороны, больше всех элементов левого поддерева, с другой стороны меньше всех значений правого поддерева.

Наша функция будет принимать в качестве аргумента узел, который необходимо удалить.

If (target->left && target->right) { //Оба наследника есть } else if (target->left) { //Есть только левый наследник } else if (target->right) { //Есть только правый наследник } else { //Нет наследников } free(target);

Если нет наследников, то нужно узнать, каким поддеревом относительно родителя является узел

If (target == target->parent->left) { target->parent->left = NULL; } else { target->parent->right = NULL; }

Если есть только правый или только левый наследник, подменяем наследником удаляемый узел. Перед этим нужно узнать, правым или левым наследником является удаляемый узел.

If (target == target->parent->left) { target->parent->left = target->left; } else { target->parent->right = target->left; }

If (target == target->parent->right) { target->parent->right = target->right; } else { target->parent->left = target->right; }

Если оба наследника, то сначала находим максимум левого поддерева

Node *localMax = findMaxNode(target->left);

Затем подменяем значение удаляемого узла на него

Target->data = localMax->data;

После чего удаляем этот узел

RemoveNodeByPtr(localMax); return; Здесь мы использовали рекурсию, хотя я обещал этого не делать. Вызов будет всего один, так как известно, что максимум не содержит обоих наследников и является правым наследником своего родителя. Если хотите заменить вызов функции, то придётся скопировать оставшийся код.

Void removeNodeByPtr(Node *target) { if (target->left && target->right) { Node *localMax = findMaxNode(target->left); target->data = localMax->data; removeNodeByPtr(localMax); return; } else if (target->left) { if (target == target->parent->left) { target->parent->left = target->left; } else { target->parent->right = target->left; } } else if (target->right) { if (target == target->parent->right) { target->parent->right = target->right; } else { target->parent->left = target->right; } } else { if (target == target->parent->left) { target->parent->left = NULL; } else { target->parent->right = NULL; } } free(target); }

Упростим работу и сделаем обёртку вокруг функции, чтобы она удаляла узел по значению

Void deleteValue(Node *root, T value) { Node *target = getNodeByValue(root, value); removeNodeByPtr(target); }

Для проверки можно ввести функцию печати дерева. Так как мы ещё не научились обходить деревья, вывод осавляет желать лучшего.

Void printTree(Node *root, const char *dir, int level) { if (root) { printf("lvl %d %s = %d\n", level, dir, root->data); printTree(root->left, "left", level+1); printTree(root->right, "right", level+1); } }

Проверка

Void main() { Node *root = NULL; insert(&root, 10); insert(&root, 12); insert(&root, 8); insert(&root, 9); insert(&root, 7); insert(&root, 3); insert(&root, 4); printTree(root, "root", 0); printf("max = %d\n", findMaxNode(root)->data); printf("min = %d\n", findMinNode(root)->data); deleteValue(root, 4); printf("parent of 7 is %d\n", getNodeByValue(root, 7)->parent->data); printTree(root, "root", 0); deleteValue(root, 8); printTree(root, "root", 0); printf("------------------\n"); deleteValue(root, 10); printTree(root, "root", 0); getch(); }

Двоичные деревья поиска или бинарные деревья(binary tree) — это структура данных, состоящая из:

• одного единственного корневого узла, который не имеет родителей;
• остальных узлов, которые имеют одного единственного родителя и не более двух потомков.

Каждый узел дерева может быть корневым узлом для одного из своих поддеревьев(subtree) . Родительский узел — это узел, который имеет одного или двух потомков. Тот узел, который не имеет потомков, называется листом или листовым узлом . Двоичные деревья поиска названы так не просто потому что каждый узел дерева может иметь два потомка. Ключ левого потомка данного узла должен быть меньше, чем значение, которое хранит этот узел. Ключ правого потомка должен быть больше значения, которое хранится в родительском узле (см.рисунок).

В общем случае структуру для хранения узла можно представить следующим образом(на языке С):

Структура, представляющая узел хранит сами данные(поле data ) и три указателя — на родительский узел, левого и правого потомков. У корневого узла дерева поле parent будет равно NULL . Сохранение ссылки на родительский узел на самом деле необязательно. Но в некоторых случаях используется.

Еще раз взгляните на рисунок выше.

Корневой узел содержит в себе значение 27. Значение, которое хранит его левый потомок должно быть меньше, чем значение родительского узла. Мы видим там число 14 (14 < 27). Правый же потомок хранит больше значение(35 > 27) и так далее. Временная сложность процедуры поиска в двоичном дереве поиска оценивается как O(logN) . Допустим, что нам нужно найти вершину с ключом, равным 31.

Для того, чтобы найти этот узел, мы сначала сравниваем его со значением в корне. Корень хранит число 27, которое не является искомым элементом(21 != 27). При этом значение искомого элемента больше(31 > 27), чем значение, хранимое в текущем узле, а это значит, что поиск следует продолжить в правом поддереве. Теперь мы пришли в узел со значением 35. Это также не то, что мы искали, поэтому мы двигаемся дальше, а именно в левое поддерево(так как 31 < 35).

В итоге мы приходим в узел со значением 31, а это именно тот элемент, который мы искали. Возможно вся эта процедура уже вам напомнила обычный двоичный поиск в упорядоченном массиве. Это действительно так. Чем же тогда такое дерево лучше обычного массива? Помимо того же преимущества в скорости поиска, бинарное дерево упрощает процедуру вставки нового элемента в середину последовательности, так как в случае с бинарным деревом нам нужно лишь поменять несколько ссылок.

Но на самом деле у двоичного дерева есть один недостаток. И в некоторых ситуациях он может оказаться довольно существенным. Двоичное дерево поиска хорошо работает со случайными данными. В наихудшем случае, при поступлении на вход заведомо отсортированных данных, мы получаем вырожденную временную сложность O(N) . Так как в этом случае элементы будут всегда вставляться только в одно поддерево. В итоге мы получим обычный связный список и потеряем все преимущества двоичного поиска.

Как решить данную проблему? Для этого используются сбалансированные деревья, вроде красно-черных деревьев, которые предотвращают подобные ситуации в принципе. Но и сложность реализации повышается. Однако порой эта сложность полностью себя оправдывает.

Теперь приведем реализацию бинарного дерева с операциями вставки нового узла и поиска.

Реализация бинарного дерева на языке С.

Еще раз приведем реализацию структуры, представляющей узел дерева:

typedef struct _Node { int data; struct Node *parent; struct Node *left; struct Node *right; } Node;

Теперь структуру, описывающую само дерево поиска. В структуре будет храниться ссылка на корень дерева и количество узлов в нем.

typedef struct _BinaryTree { Node *root; int size; } BinaryTree;

Напишем метод для создания нового дерева, который вернет указатель на созданное дерево.

BinaryTree *createTree() { BinaryTree *tree = (BinaryTree*)malloc(sizeof(BinaryTree)); tree->size = 0; tree->root = NULL; }

Добавление нового узла.

Теперь реализуем метод для добавления нового элемента в дерево. Если дерево еще пусто(root указывает на NULL ), то создаем корень дерева, если нет, то сравниваем значение, которое должен хранить новый элемент со значением текущего узла. Если оно меньше, то двигаемся в левое поддерево, а если больше — в правое, пока не найдем пустой узел, в который можно будет добавить данные:

//добавление нового узла Node *addNode(BinaryTree *tree, int data) { Node *newNode = (Node*)malloc(sizeof(Node)); newNode->data = data; newNode->left = NULL; newNode->right = NULL; if(tree->root == NULL) { tree->root = newNode; tree->size++; return newNode; }else { Node *currentNode = tree->root; Node *parent; while(true) { parent = currentNode; if(data < currentNode->data) { //идем в левое поддерево currentNode = currentNode->left; //нашли пустой узел? if(currentNode == NULL) { //добавляем сюда новый узел parent->left = newNode; tree->size++; return newNode; } }else { //идем в правое поддерево currentNode = currentNode->right; //нашли пустой узел? if(currentNode == NULL) { //добавляем сюда новый узел parent->right = newNode; tree->size++; return newNode; } } } } }

Данный метод возвращает указатель на добавленный узел дерева.

Теперь мы можем создать новое дерево и добавить туда несколько элементов.

BinaryTree *tree = createTree(); printf("%s = %i\n", "Count:", tree->size); addNode(tree, 50); addNode(tree, 10); addNode(tree, 75);

Поиск узла с заданным ключом.

Поиск узла в двоичном дереве подразумевает перемещение по дереву и сравнение искомого ключа с ключами, которые хранятся в каждом узле. При каждом сравнении возможны три различные ситуации:

1). Значение ключа совпадает со значением в просматриваемом узле. Значит, элемент найден и мы возвращаем указатель на него.

2). Значение ключа меньше, чем значение, которое хранится в текущем узле. Значит, нужно продолжить поиск в левом поддереве. currentNode = currentNode->left .

3). Значение ключа больше, чем значение, которое хранится в текущем узле. Значит, нужно продолжить поиск в правом поддереве. currentNode = currentNode -> right .

Теперь приведем реализацию самой функции поиска. Если элемент найден не будет, то функция вернет значение NULL .

//поиск узла Node *search(BinaryTree *tree, int key) { Node *currentNode = tree->root; while(currentNode->data != key) { if(key < currentNode->data) currentNode = currentNode->left; else currentNode = currentNode->right; if(currentNode == NULL) return NULL; } return currentNode; }

Обход дерева.

Процедурой обхода дерева называется посещение всех узлов дерева по одному разу в определенном порядке. Существует три разных порядка обхода: прямой , центрированный (симметричный) и обратный. Мы рассмотри здесь реализацию наиболее часто используемой процедуры обхода, а именно симметричного порядка обхода. Реализовав данный тип обхода вы с легкостью реализуете два оставшихся. Центрированный порядок обхода подразумевает посещение сначала двух потомков некоторого узла, а затем самого узла. В итоге он обрабатывает узлы дерева в порядке возрастания. Другие два типа обхода используются в разборе алгебраических выражений.

Так как деревья сами по себе обладают рекурсивной структурой, то и обход мы также выполним с применением рекурсии. Итак, наш алгоритм будет состоять из следующих шагов:

1). Обход левого поддерева.

2). Посещение узла(подразумевает какие-то операции над узлом, в нашем случае это просто вывод значения, хранимого в узле на экран).

3). Обход правого поддерева.

Данный алгоритм очень легко реализуется:

//симметричный обход дерева void inorder(BinaryTree *tree, Node *localRoot) { if(localRoot != NULL) { inorder(tree, localRoot->left); printf("%i -> ", localRoot->data); inorder(tree, localRoot->right); } }