Уравнение - это два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестными. Решить уравнение - значит найти все значения неизвестных, при которых оно обращается в верное равенство, или установить, что таких значений нет.

В школьном курсе, как правило, рассматривают уравнения, в которых неизвестные принимают числовые значения. Числовое значение неизвестного, удовлетворяющее уравнению с одним неизвестным, называется корнем или решением этого уравнения. Набор чисел, удовлетворяющих уравнению с несколькими неизвестными, называется его решением.

В математике рассматривают также уравнения, в которых неизвестными являются целые числа (диофантовы уравнения), векторы (векторные уравнения), функции (дифференциальные, интегральные, функциональные уравнения) и объекты другой природы. Вместе с уравнением указывают его область определения (множество допустимых значений неизвестных); если это не сделано, то предполагается, что это - естественная общая область определения выражений, стоящих в левой и правой частях уравнения.

Уравнение - одно из важнейших понятий математики. В большинстве практических и научных задач, где какую‑то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается составить соотношение (или несколько соотношений), которым оно удовлетворяет. Так получают уравнение (или систему уравнений) для определения неизвестной величины.

Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры. Привычная нам буквенная запись уравнений окончательно сложилась в XVI в.; традиция обозначать неизвестные последними буквами латинского алфавита $x,y,z,…,$ а известные величины (параметры) - первыми $a,b,c,…$ идет от французского ученого Р. Декарта.

Обычный путь алгебраического (чаще говорят, аналитического) решения уравнения состоит в том, что с помощью преобразований его сводят к более простым уравнениям. Если все решения одного уравнения являются решениями другого, то второе уравнение называется следствием первого. Если каждое из двух уравнений - следствие другого (т. е. множества их решений совпадают), то такие уравнения называются равносильными. Применяя к обеим частям уравнения одно и то же преобразование, мы приходим к следствию этого уравнения. Если же это преобразование обратимо, то получается уравнение, равносильное данному. (Например, умножая обе части уравнения на одно и то же число, мы получаем следствие данного уравнения. Если это число отлично от нуля, то выполненное преобразование обратимо, так что полученное уравнение равносильно исходному).

Решая уравнение с одним неизвестным, мы пытаемся прийти к простейшим уравнениям, для решения которых есть готовые формулы. Это линейные уравнения, квадратные уравнения, уравнения вида $φ(x)=c$, где $c$ - число, а $φ$ - одна из основных элементарных функций: степенная $\varphi (x)={{x}^{n}}$, показательная $\varphi (x)={{a}^{x}}$, логарифмическая $\varphi (x)={{\log }_{a}}x$, тригонометрические $\varphi (x)=\sin x$, $\varphi (x)=\cos x$, $\varphi (x)=\mathrm{tg}\, x$.

Заметим, что запись общего решения уравнения $φ(x)=c$ требует введения функции $ψ$, обратной к функции $φ$. Если $\varphi (x)={{x}^{n}}$, то $\psi (c)=\sqrt[n]{c}$; если $\varphi (x)={{a}^{x}}$, то $\psi (c)={{\log }_{a}}c$; если $\varphi (x)=\sin x$ и $−π/2≤x≤π/2$, то $\psi (c)=\arcsin x$.

Как же сводятся уравнения к простейшим? Для конкретного типа уравнений (алгебраических, тригонометрических, иррациональных, показательных, логарифмических и т.п.) разработаны частные приемы решения. Из общих методов решения уравнений остановимся на трех, которые встречаются чаще всего.

Если левую часть уравнения $f(x)=0$ удается разложить на множители: $f(x)={{f}_{1}}(x)\cdot \ldots \cdot {{f}_{m}}(x),$ то оно распадается на уравнения ${{f}_{1}}(x)=0,$ ${{f}_{2}}(x)=0 …,$ ${{f}_{1}}(x)=0,$ объединение множеств их решений дает множество решений данного уравнения. Например, уравнение ${{x}^{3}}-7x+6=0$ можно решить так: $({{x}^{3}}-x)-(6x-6)=0,$ $x(x-1)(x+1)-6(x-1)=0,$ $(x-1)({{x}^{2}}+x-6)=0.$ Решая уравнения $x−1=0$ и ${{x}^{2}}+x-6=0,$ находим все корни данного уравнения: $1, 2$ и $−3.$ Этот метод принято называть методом разложения на множители.

Часто удается упростить уравнение, принимая в качестве новой неизвестной некоторую функцию от старой неизвестной. Например, уравнение $\sin x+\cos x=\sin 2x$ можно свести к квадратному уравнению, положив $y=\sin x+\cos x.$ Тогда $\sin 2x={{y}^{2}}-1,$ и мы приходим к уравнению ${{y}^{2}}-y-1=0.$

Иногда удается решить уравнение, анализируя функциональные свойства его левой и правой частей.

Например, так как левая часть уравнения ${{2}^{x}}+{{3}^{x}}=5$ возрастает, а правая - постоянна, то это уравнение не может иметь более одного корня. Единственный корень $x=1$ легко угадывается.

Решая уравнение ${{\sin }^{3}}x+{{\cos }^{5}}x=\sqrt{2},$ заметим, что при всех $x$ выполняются неравенства ${{\sin }^{3}}x\le {{\sin }^{2}}x,$ $co{{s}^{5}}x\le {{\cos }^{2}}x,$ откуда $si{{n}^{3}}x+{{\cos }^{5}}x\le$ ${{\sin }^{2}}x+{{\cos }^{2}}x=1,$ а так как $\sqrt{2}>1,$ то данное уравнение не имеет корней.

Уравнение. Рис. 1.

Уравнение. Рис. 2.

До сих пор мы разбирали приемы решения уравнений, позволяющие найти корень уравнения как число или комбинацию известных функций от параметров. Однако далеко не все уравнения, возникающие на практике, можно решить подобным образом. Например, в начале XIX в. было доказано, что не существует общей формулы для решения алгебраических уравнений начиная с пятой степени. Да и в тех случаях, когда уравнение удается решить, формула для корней может быть чересчур громоздкой. Поэтому в математике разработаны различные методы приближенного решения уравнений. Простейший из них основан на том, что если функция $f(x)$ непрерывна во всех точках отрезка $$ и принимает на его концах значения разных знаков, то уравнение $f(x)=0$ имеет на этом отрезке корень.

Приближенное решение уравнений тесно связано с построением графиков функций.

Например, построив график функции $y={{x}^{3}}+x,$ мы можем заключить, что уравнение ${{x}^{3}}+x=1$ имеет один корень и этот корень лежит на отрезке $$, более точно - на отрезке $$, еще более точно - на отрезке $$ (рис. 1). Эта информация практически более полезна, чем точная формула Кардано, выражающая этот корень:

$\sqrt{\frac{1}{2}+\sqrt{\frac{1}{4}+\frac{1}{27}}}+\sqrt{\frac{1}{2}-\sqrt{\frac{1}{4}+\frac{1}{27}}}$

(все равно извлекать радикалы можно лишь приближенно). Для отыскания корней с любой степенью точности» существуют «быстрые» алгоритмы, основанные на методе последовательных приближений (см. Приближенные вычисления).

С помощью графика особенно удобно проводить исследование уравнений; например, по графику $y={{x}^{3}}-x$ (рис. 2) мы сразу видим, что уравнение ${{x}^{3}}-x=c$ имеет три корня при $\left| c \right| 2/\sqrt{3}.$

Уравнение – одно из краеугольных понятий всей математики. Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. :) Так что же такое уравнение?

То, что это слово однокоренное со словами "равный", "равенство", возражений, думаю, ни у кого не вызывает.

Уравнение – это два математических выражения, соединённых между собой знаком "=" (равно).

Но… не каких попало. А таких, в которых (хотя бы в одном) содержится неизвестная величина . Или, по-другому, переменная величина. Или, сокращённо, просто "переменная". Которая обычно обозначается буквой "х" .

Переменных может быть одна, может быть несколько. В школьной математике чаще всего рассматриваются уравнения с одной переменной. И мы тоже пока что будем рассматривать уравнения с одной переменной. С двумя переменными или более – в специальных уроках.

Что значит решить уравнение?

Переменная, входящая в уравнение, может принимать любые допустимые математикой значения. На то она и переменная. :) При каких-то значениях переменной получается верное числовое равенство, а при каких-то – нет.

Так вот:

Решить уравнение означает найти ВСЕ такие значения переменной, при подстановке которых в исходное уравнение получается верное равенство. Или, более научно, верное тождество. Или доказать, что таких значений переменной не существует.

Что такое верное равенство? Это равенство, не вызывающее сомнений даже у человека, абсолютно не отягощённого глубокими математическими познаниями. Например, 5=5, 0=0, -10=-10. И так далее. :)

Значения переменной, при подстановке которых достигается это самое верное равенство , называются очень красиво и научно - корни уравнения .

Корень может быть один, может быть несколько. А может быть и бесконечно много корней – целый интервал или даже вообще вся числовая прямая от –∞ до +∞ . Да, такое тоже бывает! Всё от конкретного уравнения зависит.)

А бывает и такое, что нельзя найти такие иксы, которые давали бы нам верное равенство. Принципиально нельзя. По определённым причинам. Нету таких иксов…

В таких случаях обычно говорят, что уравнение не имеет корней.

Для чего нужны уравнения?

Вопрос смешной. Для жизни! В школе, как правило, уравнения нужны для решения текстовых задач . Это, напоминаю, задачи , на работу, на проценты и многие другие.

А во взрослой жизни без уравнений невозможны было бы ответить даже на самые обычные, но жизненно важные вопросы повседневности: какая будет погода завтра, выдержит ли заданную нагрузку здание. Или лифт. Или самолёт. Куда попадёт ракета… И не было бы сейчас среди нас ни синоптиков, ни инженеров, ни бухгалтеров, ни экономистов, ни программистов… За ненадобностью. Внушает?)

Почему это так? А потому, что уравнениями описываются почти все известные человеку природные явления и процессы. Изменение давления и температуры воздуха с высотой, закон всемирного тяготения, размножение бактерий, радиоактивный распад, химические реакции, электричество, спрос и предложение – в основе всего этого лежат математические уравнения! Простые, сложные – всякие. Какое явление или ситуация, такое и уравнение.)

Итак, запоминаем:

Уравнения – очень мощный и универсальный инструмент для решения самых разных прикладных задач.

А какие бывают уравнения?

Уравнений в математике несметное количество. Самых разных видов. Но всё многообразие уравнений можно условно разделить всего на 4 категории:

1. ,

2. ,

3. (или дробно-рациональные),

4. Прочие.

Разные категории уравнений требуют и разного подхода к их решению: линейные уравнения решаются одним способом, квадратные – другим, дробные – третьим, тригонометрические, логарифмические, показательные и прочие – тоже решаются своими методами.

Прочих уравнений, разумеется, больше всего, да...) Это и иррациональные, и тригонометрические , и , и , и многие другие уравнения. И даже дифференциальные уравнения (для студентов), где роль неизвестного играет не число, а функция. Или даже семейство функций. :)

В соответствующих уроках мы подробно разберём все эти типы уравнений. А здесь у нас – базовые приёмы и правила.

Называются эти правила – тождественные (или – равносильные) преобразования уравнений . Их всего два. И нигде их не обойти. Так что знакомимся!

Как решать уравнения? Тождественные (равносильные) преобразования уравнений.

Решение любого уравнения заключается в поэтапном преобразовании входящих в него выражений. Но преобразований не абы каких, а таких, чтобы от шага к шагу суть всего уравнения не менялась . Несмотря на то, что после каждого преобразования уравнение будет видоизменяться и, в конечном счёте, станет совсем не похоже на исходное.

Такие преобразования в математике называются равносильными или тождественными . Их довольно много, но среди всего многообразия тождественных преобразований уравнений выделяется два базовых . О них и пойдёт речь в этом уроке. Да-да, всего два! Но – крайне важных! И каждое из них заслуживает отдельного внимания.

Применение этих двух тождественных преобразований в том или ином порядке гарантирует успех в решении 99% уравнений математики. Заманчиво, правда?

Итак, вперёд!

Первое тождественное преобразование:

К обеим частям уравнения можно прибавить (или отнять) любое (но одинаковое!) число или выражение (в том числе и с переменной). Суть уравнения от этого не изменится.

Это преобразование вы применяете всюду, наивно думая, что переносите какие-то члены из одной части уравнения в другую, меняя знаки. :)

Например, такое крутое уравнение:

Тут и думать нечего, перебрасываем тройку вправо, меняя минус на плюс:

А что же происходит в действительности? А на самом деле вы… прибавляете к обеим частям уравнения тройку!

Вот что у вас происходит:

И результат получается тем же самым:

Вот и всё. Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа – что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!

Дело в том, что привычный нам перенос слагаемых из одной части в другую со сменой знака – это просто сокращённый вариант первого тождественного преобразования.

И зачем нам так глубоко копать? В уравнениях – незачем. Переносите себе спокойно и не парьтесь. Только знаки менять не забывайте.) А вот в неравенствах привычка к переносу может и слегка обескуражить, да…

Это было первое тождественное преобразование. Переходим ко второму.

Второе тождественное преобразование:

Обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение.

Это тождественное преобразование мы вы постоянно применяете, когда решаете что-нибудь совсем уж жуткое типа:

Тут каждому ясно, что х=3 . А вот как вы получили этот ответ? Подобрали? Угадали?

Чтобы не подбирать и не гадать (мы с вами математики, а не гадалки), нужно понять, что вы просто поделили обе части уравнения на четвёрку. Которая нам и мешает.

Вот так:

Эта палка с делением означает, что на четвёрку делятся обе части нашего уравнения. Через дроби эта процедура выглядит так:

Слева четвёрки благополучно сокращаются, остаётся икс в гордом одиночестве. А справа при делении 12 на 4 получается, понятное дело, тройка. :)

И все дела.)

Звучит невероятно, но эти два (всего два!) простых преобразования лежат в основе решения всех уравнений математики! Да-да, именно всех , я нисколько не преувеличиваю! От линейных и квадратных в школе до дифференциальных в ВУЗе.)

Ну что, посмотрим на тождественные преобразования уравнений в действии?

Применение тождественных преобразований к решению уравнений.

Начнём с первого тождественного преобразования. Переноса вправо-влево.

Пример для новичков:

1 – х = 3 – 2х

Дело нехитрое. Это . Работаем прямо по заклинанию: "С иксами влево, без иксов – вправо".

Эта мантра – универсальная инструкция по применению первого тождественного преобразования. Вот и смотрим на уравнение. Какое слагаемое с иксом у нас справа? Что? 2х ? Не-а!) Справа у нас -2х (минус два икс)! Поэтому при переносе в левую часть минус поменяется на плюс:

1 – х +2х = 3

Полдела сделано, иксы собрали слева. Осталось все числа собрать справа. Слева в уравнении стоит единичка. Опять вопрос – с каким знаком? Ответ "с никаким" не катит.) Слева перед единицей и вправду ничего не написано. А это значит, что перед ней стоит знак "плюс" . Так уж в математике повелось: ничего не написано – значит, плюс.)

И поэтому вправо единичка перенесётся уже с минусом :

-х + 2х = 3 - 1

Вот почти и всё. Слева приводим подобные, а справа – считаем. И получаем:

х = 2

Это было совсем примитивное уравнение.

Теперь пример покруче, для старшеклассников:

Решить уравнение:

Уравнение . Ну и что? Какая разница? Всё равно первым шагом делаем базовое тождественное преобразование ("С иксами влево ….") . Для этого слагаемое с иксом (то есть, - log 3 x ) переносим влево. Со сменой знака:

А числовое выражение (log 3 4 ) переносим вправо. Также со сменой знака, разумеется:

Вот и всё. Справа получилась чистая формула. Кто дружит с , тот в уме дорешает уравнение и получит:

х=3

Что? Хотите синусы? Пожалуйста, вот вам синусы:

И снова всё то же самое! Выполняем первое тождественное преобразование – переносим sin x влево (с минусом), а -0,25 переносим вправо (с плюсом):

Получили простейшее тригонометрическое уравнение с синусом, решить которое (для знающих) также не составляет никакого труда.

Видите, насколько универсально первое равносильное преобразование! Встречается везде и всюду и не обойти его никак… Именно поэтому так важно уметь его делать на автомате и без ошибок.

Собственно, ошибиться здесь можно лишь в одном – забыть сменить знак при переносе. Что и происходит сплошь и рядом. Внимательность никто не отменял, да…)

Ну что, продолжаем наши игры? Развлекаемся теперь со вторым преобразованием!)

Решить уравнение:

7х=28

Крутяк, прямо скажем.) Ладно, это эмоции…

Смотрим и соображаем: что нам мешает в этом уравнении? Что-что… Да семёрка мешает! Хорошо бы от неё избавиться. Да так, чтобы исходное уравнение не испортить.)

Но как? Перенести вправо? Ээээ… Стоп! Нельзя.) Семёрка с иксом умножением связана. Коэффициент, видите ли.) Нельзя её оторвать от икса и вправо перенести. Вот всё выражение 7х целиком – пожалуйста (вопрос – зачем?). А семёрку отдельно – никак нет.

Самое время про умножение/деление вспомнить! Нам ведь в ответе чистый икс нужен, не так ли? А семёрка – мешает. Вот и делим левую часть на семь. "Очищаем" икс от коэффициента. Так нам надо. Но тогда и правую часть тоже надо поделить на семь: этого уже математика требует. Что уж там получится, то и получится. Но пример хороший. Я старался.) 28 на 7 замечательно делится. Получится 4.

Ответ: х=4

Или такое уравнение:

Что здесь нам мешает? Дробь 1/6, не так ли? Вот давайте и избавимся от неё. Безопасно для уравнения.) Как? Ну, можно поступить аналогично – поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…

Но мы же не только делить, мы ещё и умножать умеем!) Вспоминаем из младших классов, после какого действия у нас пропадает дробь? Правильно! Дробь у нас пропадает при умножении на число, равное (или кратное) её знаменателю. Вот и умножим обе части нашего уравнения на 6. Слева всё равно чистый икс получится, а умножение правой части на 6 – не самая трудная работа.)

Вот и всё.) Умножение обеих частей уравнения на нужное число позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, запросто можно и ошибок наляпать. Короче дорога – меньше ошибок!

Теперь снова на машину времени и - в старшие классы:

Решить уравнение:

Чтобы добраться до икса и тем самым решить это крутое тригонометрическое уравнение , нам надо сначала получить слева чистый косинус, безо всяких коэффициентов. А двойка мешает. :) Вот и делим на 2 всю левую часть:

Но тогда и правую часть тоже придётся разделить на двойку: это уже МАТЕМАТИКЕ надо. Делим:

Получили справа табличное значение косинуса . И теперь уравнение решается за милую душу.)

Вот и вся премудрость. Как видите, тождественные преобразования уравнений – штука полезная. И при этом не самая сложная. Перенос да умножение/деление. Однако далеко не у всех они получаются с первого раза и без ошибок, ох не у всех… Основные проблемы здесь две.

Проблема первая (для малоопытных):

Иногда ученик думает, что упрощение уравнений делается по одному, раз и навсегда установленному правилу. И никак не может уловить и понять это правило: в каких-то примерах начинают с домножения (или деления), в каких-то – с переноса. Где-то три раза переносят и ни разу не домножают…

Например, такое линейное уравнение:

10х + 5 = 5х – 20

С чего начинать? Можно начать с переноса:

10х – 5х = -20 - 5

А можно сначала поделить обе части на пятёрку, а затем уж переносить. Тогда сразу числа попроще станут:

Как видим, и так и сяк решать можно. И это – в примитивном примере! Вот и возникает у неопытных учеников вопрос: "Как правильно?"

По-всякому правильно! Кому как удобнее. :) Универсального рецепта здесь нет и быть не может. Математика предлагает вам на выбор два вида преобразований уравнений. А порядок этих самых преобразований зависит исключительно от исходного уравнения, а также от личных предпочтений и привычек решающего.

Проблема вторая (для всех...ну… почти):

Ошибки в вычислениях. В преобразованиях постоянно приходится перемножать скобки. Заключать выражения в скобки и раскрывать скобки. Умножать и делить дроби. Работать со степенями… Короче, в наличии весь набор элементарных действий математики. Со всеми вытекающими…

Обе эти проблемы устраняются только одним способом – практикой. Исчезают сомнения и ошибки. Примеры становятся проще, задания - легче. И в итоге не математика командует вами, а вы – математикой. :)

Линейная структура управления является наиболее приемлемой лишь для простых форм организаций. Отличительная черта: прямое воздействие на все элементы организации и сосредоточение в одних руках всех функций руководства. Структура хорошо работает в небольших организациях при высоком профессионализме и авторитете руководителя.

В небольших организациях с четким распределением функциональных обязанностей получили также распространение структуры в виде кольца, звезды и колеса. организационный структура линейный матричный

Линейная структура управления: кольцо

Р - руководитель;

И - исполнитель

Линейная структура управления: звезда

Р - руководитель;

И - исполнитель

Линейная структура управления: колесо

Р - руководитель;

И - исполнитель

Линейно-функциональная структура управления основана на так называемом "шахтном" принципе построения и специализации управленческого процесса в зависимости от обязанностей, возложенных на заместителей руководителя - функциональных руководителей. К их числу относятся: коммерческий директор, заместители директора по кадрам, по производству, руководители информационного отдела, отдела маркетинга и т.д.

Линейно-функциональная структура управления

Линейно-штабная структура управления представляет собой комбинированную структуру, сочетающую свойства линейных и линейно-функциональных структур. Она предусматривает создание специальных подразделений (штабов) в помощь линейным руководителям для решения тех или иных задач. Эти штабы готовят руководителю проекты решений по соответствующим вопросам. Штабы не наделяются исполнительной властью. Руководитель сам принимает решение и доводит его до всех подразделений. Штабная схема наиболее целесообразна, если необходимо осуществлять линейное управление (единоначалие) по ключевым позициям организации.

Линейно-штабная структура управления

Матричная структура управления представляет собой решетчатую организацию, построенную на принципе двойного подчинения исполнителей: с одной стороны, непосредственному руководителю функциональной службы, которая предоставляет персонал и техническую помощь руководителю проекта, с другой - руководителю проекта (целевой программы), который наделен необходимыми полномочиями для осуществления процесса управления в соответствии с запланированными сроками, ресурсами и качеством. Матричная схема применяется при сложном, наукоемком производстве товаров, информации, услуг, знаний.

Программно-целевая структура управления предусматривает создание специальных органов управления краткосрочными и долгосрочными программами. Она ориентирована на обеспечение всей полноты линейных полномочий в рамках реализуемых программ.

Матричная структура управления

Продуктовая структура управления является одним из вариантов программно-целевой структуры. Она предусматривает возложение на руководителя, ответственного за программу выпуска конкретного продукта, всей ответственности за качество и сроки выполнения работ. Этот руководитель наделяется всеми правами распоряжения в части производственной, сбытовой и вспомогательной деятельности, связанной с изготовлением конкретного продукта или ассортимента продуктов.

Проектная структура управления формируется при разработке организацией проектов, под которыми понимаются любые процессы целенаправленных изменений в системе управления или в организации в целом, например, модернизация производства, освоение новых технологий, строительство объектов и т.п. Управление проектом включает определение его целей, формирование структуры, планирование и организацию работ, координацию действий исполнителей. Одной из форм проектного управления является формирование специального подразделения - проектной команды, работающей на временной основе.

Функционально-объектная структура управления предусматривает выделение в функциональных подразделениях наиболее квалифицированных специалистов, которые в дополнение к их функциональным обязанностям назначаются руководителями конкретных работ или объектов в данном подразделении. Внутри подразделения эти специалисты являются старшими при выполнении порученной работы не только в рамках постоянно закрепленных за ними функций, но и по всем другим вопросам.

Разновидностью иерархического типа организации управления является весьма сложная и разветвленная структура, получившая название дивизиональной структуры управления (от английского слова division - отделение), первые разработки которой относятся к 20-м годам, а пик практического использования - к 60-70-м годам ХХ столетия.

Необходимость новых подходов к организации управления была вызвана резким увеличением размеров предприятий, диверсификацией их деятельности и усложнением технологических процессов в условиях динамично меняющейся внешней среды. Первыми перестройку структуры по этой модели начали крупнейшие организации, которые в рамках своих гигантских предприятий (корпораций) стали создавать производственные отделения, предоставив им определенную самостоятельность в осуществлении оперативной деятельности. При этом администрация оставляла за собой право жесткого контроля по общекорпоративным вопросам стратегии развития, научно-исследовательских разработок, инвестиций и т.д. Поэтому этот тип структуры нередко характеризуют как сочетание централизованной координации с децентрализованным управлением (децентрализация при сохранении координации и контроля).

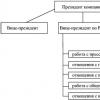
Ключевыми фигурами в управлении организациями с дивизиональной структурой становятся не руководители функциональных подразделений, а менеджеры, возглавляющие производственные отделения. Структуризация организации по отделениям производится, как правило, по одному из трех критериев:

• - по выпускаемой продукции или предоставляемым услугам (продуктовая специализация);
• - по ориентации на потребителя (потребительская специализация);
• - по обслуживаемым территориям (региональная специализация).

В результате расширения границ оперативно-хозяйственной самостоятельности отделения могут рассматриваться как "центры прибыли", активно использующие предоставленную им свободу для повышения эффективности работы.

В то же время дивизиональные структуры управления приводят к росту иерархичности, т.е. вертикали управления, связанной с необходимостью формирования промежуточных уровней менеджмента для координации работы отделений, групп и т.п., в которых управление строится по линейно-функциональному принципу. Дублирование функций управления на разных уровнях приводит к росту затрат на содержание управленческого аппарата.

Переход к дивизиональной ОСУ был значительным шагом вперед к созданию условий для ускорения научно - технического развития производства. Руководители высшего звена стали больше уделять внимания вопросам перспективного развития производства. Децентрализация оперативного управления производством стала сочетаться с жесткой системой финансового контроля и с централизацией НИОКР. Однако, наряду с положительными моментами проявились и негативные стороны дивизиональных структур. Открывшиеся возможности для расширения ассортимента выпускаемой продукции вызвали в ряде фирм усиление диверсификации производства. Этот процесс в его экстремальной форме привел к появлению фирм-конгломератов, занимающихся производством совершенно разных по своему характеру видов продукции, руководствуясь лишь стремлением обеспечить наибольшие прибыли. Многие из них в условиях ухудшения общего экономического положения и усиления конкуренции потеряли управляемость и потерпели банкротство. Также серьезным недостатком дивизиональной ОСУ явилось увеличение затрат на содержание административно-управленческого персонала. Опыт многих крупных компаний показал, что дивизиональная ОСУ может способствовать повышению эффективности управления лишь до определенных пределов, после чего начинают ощущаться все большие трудности. Основной их причиной является замедленность процесса подготовки и принятия решения, что характерно и для линейно-функционального типа ОСУ. Процесс формирования дивизиональных структур в крупных компаниях сопровождался созданием подразделений, которые наделялись значительной хозяйственной самостоятельностью.

Такие подразделения именовались отделениями и формировались главным образом по продуктовому признаку, реже по региональному или по рыночному. В американском менеджменте этот подход получил название "централизованная координация - децентрализованная администрация". Такие отделения постепенно развиваясь послужили основой современных центров. То есть, прежде всего, центров прибыли, центров реализации, центров инвестиции и т.д. По мере развития концепции стратегического управления такие центры постепенно стали трансформироваться в стратегические хозяйственные центры (СХЦ) - внутрифирменные подразделения, отвечающие одновременно и за развитие будущего потенциала. Основная проблема при создании СХЦ - это распределение ответственности, то есть организации отвечают не только за планирование и реализацию стратегии, но и за конечный результат - получение прибыли.

Одной из самых главных проблем ОСУ постепенно становилась про-блема гибкости. Эту проблему пытались решить, создавая новые варианты комбинированных структур путем внедрения в основной костяк (например, линейно-функциональной) структуры новых элементов, что вызвало к жизни новые ОСУ, такие как с временными (создаваемыми на срок) органами, с комитетами, управление по проекту (продукту, объекту), матричные структуры и т.д. Все эти варианты ОСУ получили общее название программно-целевых структур. При этом роль и место руководителя программы меняется в зависимости от условий, в которых осуществляется управление. Необходимо отметить сущностное отличие ОСУ программно-целевого типа от структур механистического типа, состоящее в том, что в основе, например, линейно-функциональной, лежит комплексное управление объективно складывающимися подсистемами, в то время как программно-целевые структуры базируются на комплексном управлении всей системой в целом, как единым объектом, ориентированным на определенную цель.

Современными модификациями программно-целевых ОСУ являются венчурные и инновационные. Крупные фирмы интегрируют такие структуры в свой менеджмент. Это наиболее перспективный путь мобильного реагирования на быстро меняющиеся условия рынка. Принципы построения и действия венчурного отдела в фирме те же, что и в самостоятельном венчурном предприятии. Венчурные (инновационные) структуры в крупных фирмах имеют несколько разновидностей в зависимости от ряда факторов:

• - значимости разрабатываемых проектов;
• - их целевой направленности и сложности;
• - от степени формализации и самостоятельности деятельности.

Таким образом, эволюция ОСУ в ХХ веке однозначно показывает, что совершенной, универсальной структуры нет и процесс поиска будет продолжаться и в новом столетии. Следует отметить, что существует и другая точка зрения, состоящая в том, что совершенной, идеальной ОСУ нет и быть не может. Это так называемая концепция "размороженной системы" или организации без ОСУ. Последователи этой концепции считают, что время "организованных организаций" прошло и что современная экономика в ХХI веке вступает в такой этап, когда особую важность приобретает самоорганизация. Не отрицая важности самоорганизации задача поиска эффективных ОСУ остается актуальной.

2) анализ технической оснащенности и методов управления.

Экономический анализ технической оснащенности и методов управления характеризует широту использования в управленческой деятельности достижений научно-технического прогресса, новых методов и эффективности управления организацией, уровень самостоятельности подразделений.

Включает в себя:

• - степень механизации и автоматизации управленческого труда
• - коэффицент эффективности управления
• - анализ методов управления
• 3) анализ состава и организации труда работников управления.

Задачи анализа организационной структуры управления заключаются:

выявлении соответствия между производственной и организационной структурами; соответствии управленческих штатов характеру и содержанию функций управления. Для этого производятся:

анализ производственной структуры предприятия;

анализ структуры органов управления;

анализ численности аппарата управления;

анализ специализации и централизации управленческих функций.