ЛЕКЦИЯ № 20

УСЛОВИЕ УПРАВЛЯЕМОСТИ И НАБЛЮДАЕМОСТИ

ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ.

План лекции:

1. Определение полностью управляемой системы.

2. Условие управляемости линейной импульсной системы.

3. Определение наблюдаемости и восстанавливаемости.

4. Условие восстанавливаемости линейной импульсной системы.

Управляемость системы определяет возможность управления со стороны входа всеми компонентами вектора состояния дискретной системы.

Система, процесс или объект называются полностью управляемыми , если они могут быть переведены из состояния x=0 в произвольное состояние x[n] с помощью управления за конечное число шагов.

Рассмотрим систему разностных уравнений:

x [ k +1]=Ф x [ k ]+ Hu [ k ]

y [ k ]= cx [ k ]+ Du [ k ] (20.1),

где x=(x 1 ,...x n)- вектор состояния;

y =(y 1 ,... y n )- вектор входных переменных;

u =(u 1 ,... u n )- вектор управления.

Предположим, что последовательность управлений имеет вид:

u , u ,... u [ n -1] . (20.2)

Тогда в соответствии с (5.44) при x =0 , получим:

x = Hu ;

x =Ф Hu + Hu ;

x = Ф 2 Hu + Ф Hu ;

. (20.3)

Найдем последовательность управлений (20.2), переводящую точку x =0 в точку x [ u ]= x . Последнее уравнение системы (20.3) также можно представить в виде:

. (20.4)

Это выражение можно рассматривать как систему линейных алгебраических уравнений относительно компонентов векторов

u [ n -1], u [ n -2] ,..., u .

Каждый вектор u имеет m скалярных компонент, так что число неизвестных равно m x n . Основная матрица системы

-

Имеет размерность (n x mn ), а расширенная матрица

Размерность (п хтп +1).

Рассмотрим условие управляемости, то есть условие существования решения (20.4).

Для существования решения системы (20.4), как известно, необходимо и достаточно, чтобы совпадали ранги основной и расширенной матриц.

Легко видеть, что так как , то . Если ранг основной матрицы меньше порядка системы п , то всегда можно так подобрать вектор Х , что ранг расширенной матрицы станет больше ранга основной матрицы.

Таким образом, чтобы система уравнений (20.4) имела решение при произвольном Х необходимо и достаточно, чтобы .Это условие полной управляемости линейной дискретной системы.

Рассмотрим случай скалярного управления и перейдем в исходной системе (5.44) с помощью преобразования

к каноническим переменным:

Окончательно получим:

,

Существуют специальные алгоритмы приведения исходной матрицы Ф к каноническому виду (диагональной форме).

Структурная схема системы приведена на рис.20.1 (при условии скалярного выхода y ).

Легко видеть, что по свойствам полной управляемости системы соответствует отсутствие нулей у вектора , то есть условия .

Наиболее распространенным алгоритмом управления систем, синтезируемых с помощью МПС, является алгоритм

.

Однако, во многих случаях состояние системы

не измеряется, и, следовательно, управление согласно вышеприведенному соотношению не может быть непосредственно реализовано.

Таким образом, возникает вопрос, можно ли определить вектор состояния по измеряемому выходу или по измеряемым выходам объекта со многими входами и многими выходами.

В этой связи в теории управления различают наблюдаемость состояния и восстанавливаемость состояния.

Состояние х (t o ) системы наблюдаемо, если оно может быть определено по будущим значениям выходной переменной y (t ), t >t 0 и если интервал t -t 0 конечен.

Состояние х (t o ) системы восстанавливаемо, если оно может быть определено по прошлым значениям выходной переменной y (t ), t >t 0 и если интервал t -t 0 конечен.

Условие наблюдаемости и восстанавливаемости можно получить из уравнения выхода системы:

и уравнения состояния:

Вычисляя последовательно значения выходной переменной для моментов времени k , k + 1,... k + n - 1, получим:

(20.5)

или в векторно-матричной форме:

или в компактной форме:

Y n [ k ]= Q p x [ k ]+ P p u [ k ].

Если матрица Q p невырожденная, то существует ее обратная матрица Q -1 P , в этом случае detQ p и строки матрицы Q p линейно независимы.

Тогда из предыдущего матричного уравнения следует:

x [k ]=Q -1 p y n [k ]- Q -1 p P p u [k ] (20.6)

Таким образом, мы можем сформулировать следующее условие наблюдаемости: линейная система, описываемая КРУ, наблюдаема, если и только если ранг матрицы Q p равен размерности n пространства состояний.

Получим условие восстанавливаемости:

Учитывая, что x [k + n ]=Ф n x [k ], то последнее матричное уравнение может быть преобразовано к виду:

Где .

Условия восстанавливаемости формулируются аналогично условиям наблюдаемости: линейная система, описываемая системой КРУ, восстанавливаема, если и только если ранг матрицы Q p равен размерности n пространства состояний.

Понятие управляемости, наблюдаемости и восстанавливаемости позволяет лучше представлять особенности динамики исследуемой системы, ее возможности. Отметим, что матрица Ф зависит от величины интервала квантования Т , поэтому свойства управляемости и наблюдаемости могут изменяться при переходе от непрерывных систем к цифровым (вспомним, например, о возможности возникновения скрытых колебаний в дискретных системах).

Таким образом, мы завершаем рассмотрение вопросов анализа динамики дискретных систем в рамках методов ПС. В настоящее время этот метод широко применяется в инженерной практике. Его развитию будет способствовать все более широкое использование ЭВМ в проектировании рассматриваемых систем, так как именно он позволяет в наибольшей степени соединить полноту и строгость теоретического исследования с возможностями современной вычислительной техники.

Управляемость и наблюдаемость линейных систем регулирования относится к основным понятиям теории автоматического регулирования, с помощью которых можно оценивать структурные схемы систем и выполнять преобразование путем ввода дополнительных сигналов или за счет их исключения. Если в системе автоматического регулирования сигнал управления сформированный в задатчике, представляет собой некоторую совокупность его составляющих превышает число степеней свободы системы, описанной уравнением то система является неуправляемой. Действительно, в этом случае систему регулирования нельзя перевести из начального состояния в любое конечное состояние под действием некоторого входного сигнала При системы автоматического регулирования именуют вполне управляемыми.

Линейную стационарную систему автоматического регулирования называют полностью управляемой, если из любого начального состояния ее можно перевести в конечное состояние при помощи входного сигнала в течение конечного интервала времени. Необходимое и достаточное условие полной управляемости линейной стационарной системы, описываемой уравнением

таково: матрица

размера первые столбцов которой состоят из элементов матрицы В, а следующие столбцов - из элементов матрицы и т. д., должна иметь ранг .

С понятием управляемости связано понятие наблюдаемости системы. Наблюдаемость позволяет установить начальное состояние системы автоматического регулирования по результатам измерений одного выходного сигнала.

Линейная стационарная система автоматического регулирования, описываемая уравнениями

полностью наблюдаема, если можно определить начальное состояние системы по следующий данным;

а) матрица А и С;

б) выходному сигналу от начальных условий при заданному на конечном интервале времени

Необходимое и достаточное условие полной наблюдаемости линейной стационарной системы заключается в том, что сопряженная матрица 1

типа должна иметь ранг

Рассмотрим два типа систем автоматического регулирования.

Первый тип - система имеет лишь один выходной сигнал

Для этой системы необходимым и достаточным условием полной наблюдаемости является отличие от нуля всех коэффициентов.

Второй тип - система имеет несколько выходных сигналов:

Тогда необходимым и достаточным условием полной наблюдаемости является то, что для каждого один из коэффициентов Он, не должен равняться нулю.

Пример IX. 15. Определить, является ли линейная стационарная система автоматического регулирования (рис. IX. 19, а) полностью неуправляемой и наблюдаемой. Составим уравнение состояния для этой системы в виде

Из уравнения (IX.253) следует, что матрица А имеет размерность

В этом случае формула (IX.251), по которой определяется управляемость, примет вид

Определитель матрицы (IX.255) будет что соответствует рангу матрицы К, меньщему 2. Для полной управляемости системы регулирования ранг матрицы К должен быть равен 2. Поэтому рассматриваемая система является неуправляемой.

Определим наблюдаемость системы регулирования. Для этого воспользуемся формулой (IX.252). В нашем случае

Рис. IX.19. Структурные схемы системы автоматического регулировании для примера IX.15

Подставив соответствующие сопряженные значения матриц в формулу (IX.256), получим

Определитель матрицы (IX.252) что соответствует рангу, меньшему 2. Для получения полной наблюдаемости системы регулирования ранг матрицы должен быть равен 2. Поэтому рассматриваемая система регулирования является ненаблюдаемой.

Этот результат становится очевидным из анализа передаточной функции замкнутой системы

Если сократить нуль в прямой цепи, когда полюс находится в цепи обратной связи, то получим

Из выражения (IX.259) можио найтн характеристическое уравнение замкнутой системы в виде

что указывает на неустойчивость системы регулирования.

• наличие хотя бы одной цели, которую принимают члены группы как общую для себя;
• наличие членов группы, которые намеренно работают вместе, чтобы достичь общей цели.

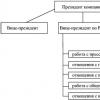
Таким образом, получается, что организация - это группа людей, которая сознательно координирует свои усилия для достижения общих целей, т. е. управляется. Управление - это целенаправленное воздействие на объект для достижения требуемого результата. Управление подразумевает наличие четырех основных элементов; вход основной системы, выход основной системы, канал обратной связи, блок управления. Такая система построена на принципе контроля результатов деятельности организации и увязке контролируемых параметров с целями на входе. Такой вид управления получил название управление по целям.

Весь процесс управления является непрерывным и состоит из четырех основных этапов. Изначально организация и ее подразделения получают задания в виде целей, под которые планируются процедуры, дающие ответ на вопросы; кто, что, где, в какие сроки и в каком количестве должен сделать. Проверка результата работы наступает после установленного срока выполнения работы. При этом оцениваются степень достижения цели и проблемы, мешавшие ее достижению. В результате контроля за результатами работы устанавливаются причины отклонения от плановых процедур и разрабатываются корректирующие мероприятия. Чтобы привести результаты к плановым, необходимо выявить природу несоответствия и при необходимости скорректировать цели. Например, если результат не был достигнут из-за некомпетентности работника, то достаточно будет применить к этому работнику санкции или заменить его, но если отклонения от намеченных результатов произошли из-за изменений во внешней среде (обвал курса рубля), необходимо корректировать цели организации или ее отдельных подразделений.

Условия управления. Оценка результатов управления - это сравнение достигнутых результатов деятельности организации в целом и ее отдельных подразделений с поставленными целями. Оценка результата управления используется как механизм обратной связи. При оценке результатов управления выявляют следующие основные параметры:

• результаты функционирования (деятельности);
• наличие ресурсов для выполнения поставленных задач;
• уровень компетентности сотрудников различных звеньев;
• степень управляемости организацией, или как слаженно функционирует вся система, где и когда происходили сбои при передаче информации и ресурсов.

Одним из наиболее важных условий надежности управления является разработка системы показателей результатов. Анализ количественных и качественных показателей способствует выявлению сильных и слабых сторон организации, помогает определить ее конкурентные преимущества (если она работает в условиях рынка), выявляет адаптационные свойства.

Основные количественные показатели:

• производственные - производительность, себестоимость, рентабельность, коэффициент сменности и т. д.;
• по персоналу - число прогулов, текучесть кадров, количество больничных листов, частота повышения квалификации и т. д.;
• финансово-экономический - прибыльность, оборачиваемость, платежеспособность, норма доходности акций и т. д.;
• рыночные (маркетинговые) - доля рынка и ее динамика, объем реализации, количество клиентов и величина потребления на одного клиента и т. д.

Основные качественные показатели:

• навыки и компетенция персонала;
• компетенция руководства;
• знание рынка;
• уровень организационной культуры;
• уровень инновационности (разработка и применение новых технологий);
• имидж организации и т. д.

В подавляющем большинстве случаев организация имеет множество различных целей. Возникает целый набор взаимосвязанных, а иногда и противоречивых целей. Многообразие целевых установок превращает организацию в сложную организацию. Например, даже не очень крупное производственное предприятие имеет цели по закупке сырья, по его переработке, по подбору персонала, по распределению готовой продукции и т. д. Все эти цели должны быть взаимоувязаны во времени, согласованы с внешними условиями. Если срывается закупка, то отдел реализации своих целей не достигает.

Общие черты организации:

• ресурсы;
• зависимость от внешней среды;
• разделение труда - горизонтальное и вертикальное;
• подразделения;
• необходимость управления.

Управление необходимо для координации всех задач, осуществляемых организацией. Управление организацией - это процесс планирования, организации, мотивации и контроля ДЛЯ того, чтобы сформулировать и достичь целей организации.

Постановка и решение задачи оптимального управления для конкретного объекта имеет смысл только в том случае, если существует принципиальная возможность перевода его из заданного начального состояния в требуемое конечное состояние за ограниченное время с использованием допустимого управления. Определение возможности такого перевода составляет содержание понятия управляемости, которое впервые было введено Р. Калманом.

Рассмотрим линейную стационарную систему, описываемую уравнением

- n - мерный вектор системы

- m - мерный вектор управления

A и B - постоянные матрицы порядка и соответственно.

Стационарная система, описываемая уравнением (1), называется управляемой, если для любых состояний и существует ограниченное измеримое управление U(t), заданное на конечном интервале , такое, что соответствующая траектория X(t) удовлетворяет условиям и .

Критерий полной управляемости системы (1), предложенный Р. Калманом, имеет простую и компактную форму. Пусть заданы матрицы A и B системы. Составим матрицу размером , в которой первые m столбцов совпадают со столбцами матрицы B, вторые m столбцов совпадают со столбцами матрицы AB и т. д., а последние m столбцов есть столбцы матрицы . Матрицу записывают так:

Управляемость линейной стационарной системы связывается со свойствами матрицы в виде следующего утверждения.

Для того, чтобы линейная стационарная система (1) была полностью управляемой, необходимо и достаточно, чтобы ранг матрицы управляемости был равен n, т.е.

Если вместо матрицы B в правой части уравнения (1) стоит матрица-столбец , т.е. m=1 и управление является скалярной функцией времени, то для полной управляемости системы необходимо и достаточно, чтобы ранг матрицы

(4) ,

имеющей размерность , был равен n, т.е. . Для полной управляемости системы в этом случае требуется, чтобы определитель матрицы не равнялся нулю, т.е. .

Если матрица A диагональна и все диагональные элементы ее различные, то система полностью управляема при условии, что матрица B не содержит нулевых строк.

Таким образом, свойство управляемости системы полностью определяется алгебраическими свойствами пары матриц {A,B}. Поэтому понятие управляемости часто относят к эти матрицам и говорят, что пара {A,B}вполне управляема или неуправляема.

Заметим, что критерий полной управляемости системы (1) никоим образом не связан с устойчивостью системы. Неустойчивая система может быть полностью управляемой и, наоборот, устойчивая система - неуправляемой. Полня управляемость означает возможность стабилизации системы, т.е. возможность построения устойчивой замкнутой системы путем присоединения соответствующего регулятора.

В случае нелинейных систем и при наличии ограничений на управление U(t) свойство управляемости может выполнятся не во всем фазовом пространстве, а критерии управляемости включают некоторые дополнительные условия. В частности доказано, что система (1), в которой на управление наложены ограничения вида

вполне управляема относительно начала координат во всем фазовом пространстве, если она при отсутствии ограничений вполне управляема и матрица A устойчива, т.е. корни уравнения имеют отрицательные вещественные части.

Рассмотрим далее понятие наблюдаемости. Чтобы управлять объектом, необходимо иметь информацию о его текущем состоянии, т.е. знать значение переменных состояния в каждый момент времени. Однако некоторые из переменных , являясь абстрактными переменными, которые вводятся для удобства и полноты описания объекта, не имеют физического аналога в реальном объекте и поэтому не могут быть измерены. Не могут быть измерены и производные высокого порядка, используемые в качестве координат состояния. Измеряются в реальном объекте некоторые переменные , которые образуют вектор Y выходных координат. Вектор Y связан определенной зависимостью с вектором состояния X. Следовательно, возникает задача восстановления текущих значений переменных состояния по результатам наблюдения за выходными переменными системы на конечном интервале времени, а также задача определения условий, при которых такое восстановление возможно. Решение этих задач и составляет содержание проблемы наблюдаемости.

Рассмотрим линейную стационарную систему

(5)

X - n - мерный вектор состояния;

U - m - мерный вектор управления;

Y - r - мерный вектор выхода, компоненты которого представляют собой реальные выходные координаты объекта;

C,D - постоянные матрицы размерностью и соответственно.

Состояние системы (5) называется полностью наблюдаемым, если можно однозначно определить по данным измерений Y(t) и U(t) на конечном интервале времени . Система (5) называется полностью наблюдаемой, если наблюдаемы все ее состояния в любые моменты времени.

Условия наблюдаемости линейной стационарной системы (5) формулируются на основе алгебраических свойств пары матриц {A,C}.

Для того, чтобы линейная стационарная система (5) была полностью наблюдаема, необходимо и достаточно, чтобы матрица

имела ранг, равный n. Если это условие не выполняется (ранг ), то система не вполне наблюдаема. Если матрица A диагональная и все диагональные элементы ее различны, то система полностью наблюдаема при условии, что матрица C не содержит нулевых столбцов.

Наиболее легко судить об управляемости и наблюдаемости объекта, если его математическая модель представлена в канонической форме.

Для примера рассмотрим математическую модель одномерного объекта в виде канонических уравнений состояния:

В скалярной форме

В векторной форме

Из этих уравнений видно, что выход объекта U(t) не оказывает влияния на переменные и . Поэтому переменные и не управляемы.

Управляемыми являются только переменные состояния и .

Переменные и не участвуют в формировании выхода Y(t). Косвенно, через переменные и , они также не влияют на выход Y(t). Поэтому переменные и не наблюдаемы на выходе, а наблюдаемыми являются только переменные состояния и .

Очевидно, что и управляемой и наблюдаемой переменной состояния является :

Этот пример показывает, что в общем случае математическая модель объекта может иметь четыре части:

1) управляемую, но не наблюдаемую часть; 2) полностью управляемую и наблюдаемую часть; 3) неуправляемую и ненаблюдаемую часть; 4) неуправляемую, но наблюдаемую часть.

Рассмотрим два случая:

а) случай неполной управляемости, но полной наблюдаемости.

На приведенной ниже схеме видно, что на часть координат не влияют входные воздействия , ни другие переменные . В данном случае часть 2 системы является неуправляемой, но наблюдаемой.

б) случай неполной наблюдаемости системы, но полной управляемости

Как видно, здесь можно найти такую систему координат, что часть из них X(2) не влияет на выходные переменные ни непосредственно, ни через другие переменные состояния X(1). В данной схеме часть 2 системы является управляемой, но не наблюдаемой.

Для определения управляемости и наблюдаемости линейных систем с обратной связью, разделяющихся на две линейные подсистемы (неизменяемая часть - объект и регулятор ),очень удобна теорема Гилберта.

Пусть линейные подсистемы и образуют систему с обратной связью согласно приведенной структурной схемы. Пусть последовательное соединение представляет собой полностью управляемую и наблюдаемую систему, а последовательное соединение неуправляемую, но полностью наблюдаемую систему. Тогда:

1) порядок системы n равен сумме порядков и , т.е. ; 2) необходимым и достаточным условием управляемости (наблюдаемости) системы с обратной связью является управляемость (наблюдаемость) ; 3) необходимым, но недостаточным условием управляемости (наблюдаемости) системы с обратной связью является управляемость (наблюдаемость) и и ; 4) если и управляемы (наблюдаемы), то любые из неуправляемых (ненаблюдаемых) координат системы с обратной связью являются неуправляемыми (ненаблюдаемыми) координатами и порождаются .

Важность данной теоремы состоит в том, что управляемость и наблюдаемость могут устанавливаться на основе исследования отдельных разомкнутых подсистем.

В случае линейных систем свойство управляемости не зависит от конкретной области в пространстве состояний.

В случае нелинейных систем и при наличии ограничений модуля вектора управления U(t) управляемость зависит от начального состояния системы и от значения составляющих вектора управления.

Рассмотренные выше понятия управляемости и наблюдаемости представляют большой интерес при синтезе оптимальных систем.

Видимо, нецелесообразно решать задачу синтеза оптимальной системы по тем координатам управления , относительно которых модель неуправляема.

С практической точки зрения наблюдаемыми переменными будут те, которые можно непосредственно измерить. Если какая-либо переменная является функцией физически наблюдаемых переменных и времени, но для ее вычисления требуются сложные вычислительные устройства, то ее считают практически наблюдаемой, хотя она по теории Калмана. Наблюдаемые на практике переменные - это те переменные, которые можно и измерять непосредственно, не используя связи, выраженные в уравнениях объекта. Этот вывод важен при решении задачи реализации закона оптимального управления.

Управляемость и наблюдаемость системы автоматизированного управления

Рассмотрим случай, когда все переменные состояния могут быть измерены, а результаты этих действий могут быть использованы для управления системой. Однако такой случай не всегда технически реализуем. Поэтому для систем автоматического управления вводится понятие управляемости.

Рассмотрим:

где - матрицы с постоянными коэффициентами.

При этом управление полагается скалярным, т.е. управление объектом осуществляется по одной координате.

Заданы начальная и конечная точка, и. Задача состоит в том, чтобы перевести систему из заданного начального положения в некоторую точку, совпадающую с началом координат. При этом никаких ограничений на величину управляющего воздействия и время регулирования не накладывается. Если такая задача решается при любых начальных и конечных условиях, то такая система является управляемой.

Система называется управляемой, если существует такое управление, которое из любого начального состояния в любое конечное положение. При каких условиях система является управляемой. Попытаемся выяснить причины неуправляемости. Это удобно сделать с помощью геометрического представления движения системы. Как отмечалось выше решение линейного однородного уравнения имеет вид:

Если какой-нибудь из коэффициентов, а остальные отличны от нуля, то движение происходит в инвариантном подпространстве матрицы. С геометрической точки зрения все траектории лежат в плоскости S, т.е. вектор также направлен вдоль этой плоскости. Предположим, что вектор тоже лежит в плоскости. Очевидно, что добавка к вектору величины оставляет вектор в той же плоскости, хотя и деформирует траекторию движения вектора состояния. Следовательно, если начальная точка лежит в плоскости, а конечная -- нет, то попасть в точку с заданными координатами нельзя, так как не существует управления, которое переводит состояние системы с заданными параметрами из начальной точки в конечную. Такая система неуправляема по определению.

Условия управляемости в терминах исходной системы получены Калманом и имеют вид:

Для управляемости системы (1) необходимо и достаточно, чтобы выполнялось условие вида

Это условие выполняется, если матрица U вида

имеет ранг, равный N.

Рангом матрицы называется наибольший порядок ее определителя, отличный от нуля.

Рассмотрим поведение системы в пространстве состояний собственных векторов матрицы А (для простоты будем полагать, что собственные значения матрицы А -- действительные и различные). Как мы убедимся в дальнейшем, в этом пространстве условия управляемости становятся практически очевидными. Введем неособое преобразование вида

Выше отмечалось, что и существует. Поэтому вектора X и Y связаны однозначной зависимостью. Следовательно, задачи об управляемости в пространствах этих переменных эквивалентны.

В пространстве новых переменных

поведение САУ описывается уравнением

Рассмотрим произведение

Следовательно, уравнение (4) приводится к виду

Вектор столбец с компонентами.

Так как матрица Р диагональная, то

и если хотя бы одно, то координата -- неуправляема. Поэтому можно предположить, что, если все, то система управляема.

Рассмотрим n-мерное пространство состояния Х, в котором каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями фазовых координат.

Пусть в пространстве состояния заданы два множества и. Рассматриваемая система будет управляемой, если существует такое управление, определенное на конечном интервале времени, которое переводит изображающую точку в пространстве Х из подобласти в подобласть.

Можно сузить определение управляемости и понимать под ней возможность перевода изображающей точки из любой области пространства состояний Х в начало координат. Система будет управляемой, если каждое состояние управляемо в этом смысле.

От пространства состояний Х перейдем к другому пространству посредством неособого преобразования, причем, где -- матрица коэффициентов.

Тогда вместо уравнения вида

где j -- матрица возмущающих и задающих воздействий,

u -- матрица-столбец управляющий величин,

y -- матрица-столбец регулируемых величин,

x- матрица-столбец фазовых координат,

будем иметь

Здесь использованы преобразованные матрицы коэффициентов:

Введение новых фазовых координат посредством неособого преобразования

приводит к эквивалентным системам различной структуры. При некотором преобразовании может оказаться, что часть управляющих величин не входит в некоторые дифференциальные уравнения (7) или часть фазовых координат не участвует в формирование вектора выходного сигнала. В первом случае система не будет полностью управляемой, а во втором -- полностью наблюдаемой.

В случае не полностью управляемой системы ее исходное уравнение могут быть представлены в виде

Это иллюстрирует рис. 7. Набор фазовых координат соответствует управляемой части фазовых координат, а набор -- неуправляемой части.

Рис. 1.

Калманом был доказан критерий управляемости, который гласит, что размерность управляющей части системы, то есть порядок первой группы уравнений (7) совпадает с рангом матрицы

где k -- размерность управляющего вектора.

При система полностью управляема, при -- система не полностью управляема, при -- система полностью не управляема.

Рис. 2.

На рис. 8 представлен простейший пример. Если рассматривать выходную величину при нулевых начальных условиях, то можно записать

определяются начальными условиям до приложения входного сигнала, а -- вынужденная составляющая. Система устойчива при.

Если начальные условия до приложения управляющего сигнала были нулевыми, то поведение системы может быть рассчитано по передаточной функции

В этом случае переходный процесс в системе определяется как

управляемость наблюдаемость автоматизированный калман

Как следует из последнего выражения, во втором случае система описывается дифференциальным уравнением не третьего, а второго порядка. Система будет устойчивой даже при.

Рассмотренная система будет не полностью управляемой. В ней оказывается, а.

При введении второй составляющей управления система оказывается полностью управляемой, и ей будет соответствовать матрица-строка передаточный функций по управлению

В случае не полностью наблюдаемой системы ее уравнения могут быть представлены в виде

Эти уравнения отличаются от (7) тем, что фазовые координаты группы не входят ни в выражения для и, ни в первое уравнение, куда входят фазовые координаты группы. Группа фазовых координат относится к ненаблюдаемым.

Калманом показано, что порядок первой группы уравнений совпадает с рангом матрицы V вида

При система полностью наблюдаема, при -- система не полностью наблюдаема, при -- система полностью ненаблюдаемая.

На рис. 9 изображен простейший пример. Для него легко показать, что в формировании выхода участвуют только две фазовые координаты из трех.

Рис. 3.

В общем случае система может содержать четыре группы фазовых координат:

управляемую, но ненаблюдаемую часть,

управляемую и наблюдаемую часть,

неуправляемую и ненаблюдаемую часть,

неуправляемую но наблюдаемую част.

Исходные уравнения системы (7) можно для самого общего случая записать следующим образом:

Левая часть характеристического уравнения

где Е -- единичная матрица размера, системы в этом случае содержит четыре сомножителя:

Управляемость и наблюдаемость системы в изложенном смысле не всегда совпадает с практическими представлениями. Даже если какая-либо фазовая координата и может быть вычислена по доступным для измерения выходным величинам обработка измеренных величин может быть, во-первых, сложной и, во-вторых, она может быть затруднена наличием помех. Поэтому практически наблюдаемыми координатами обычно считаются те из них, которые могут быть измерены датчиками различных типов.