Алгоритмические методы оптимизации процессов производства. Методы оптимизации технологических процессов. Список использованной литературы
Введение
В настоящее время все более актуальными становятся задачи оптимизации, поиска, реализации распределенных и (или) параллельных систем. Многие из них легко реализуемы простыми классическими методами, но некоторые задачи требуют к себе особого подхода. Эти задачи либо не разрешимы простыми методами, либо их решение потребует значительного времени и объема ресурсов. Для решения подобного рода задач существуют особые методы и алгоритмы.
Алгоритм культурного обмена стал признанной методикой оптимизации, которая может конкурировать с почти всеми известными методиками и, которая, благодаря своей гибкости, может превосходить множество классических методик.
Целью выполнения данной работы является описание алгоритма культурного обмена и проведение экспериментального исследования средней трудоемкости алгоритма случайного поиска версии 3.20.
К работе прилагаются три приложения А, Б и В. В них приведены данные эксперимента в виде таблиц, а также графики зависимости функции качества(Fэ) от генотипа(N).
В пункте 1 - определяется ряд задач, которые необходимо решить в курсовой работе, описываются начальные условия.
В пункте 2 - приведено описание алгоритма TS, а также примеры использования его для решения ряда проблем оптимизации.
В пункте 3 - проведено экспериментальное исследование средней трудоемкости алгоритма.
Постановка задачи
Дан алгоритм оптимизации функций рациональных переменных - алгоритм культурного обмена (КО). КО имеет следующие фиксированные параметры:
Способ кодирования решения в генотипе: двоичное представление параметра, точность представления параметра (аргумента) функции принимается, если не задана для функции специально, равной = 0.01;
Длина генотипа: определяется способом кодирования решения.
Размер популяции: 120 индивидуумов;
Доля родителей от размера популяции: 1.0, т.е. количество родителей, участвующих в кроссовере равно 120.
Кроссовер: равномерно распределенный 2-х точечный. Т.е. хромосома разбивается в двух точках, причем положения точек разбиения не фиксировано, а равномерно распределены по генотипу.
Мутация: применяется к каждому новому индивидууму, к каждому гену.
Отбор в следующее поколение: элитный отбор.
Необходимо провести экспериментальное исследование средней трудоемкости алгоритма
Алгоритм оптимизации
Описание алгоритма оптимизации
Для культурного алгоритма, основанного на эволюционном программировании для решения ограниченных проблем оптимизации.
Такой подход позволяет включение знаний об этой проблеме во время поиска. Такие знания включение позволяет значительному сокращению числа фитнес-функций оценки требуемых алгоритму.
Справочная информация культурной эволюции общества позволяет развиваться и адаптироваться к среде на более высокий уровень, чем биологической эволюции основаны Преимущества и недостатки на генетических наследование только коммуникационный протокол и с течением времени люди разработали уникальный набор возможностей, которые поддерживают алгоритм формирования, Кодирования и передачи общие черты культурной информации.
Культура есть система символически кодируется концептуальных методов явления, которые являются социально и исторически, передаваемых в рамках Преимущества и недостатки культурных алгоритмов вычислительных моделей культурной эволюции протокола и связи. Другие методы культурных алгоритмов эволюционных алгоритмов, которые поддерживают будущие направления дополнительного механизма для извлечения информации в ходе исполнения приложения алгоритма, избегая необходимости кодирования
Алгоритм уменьшает необходимость для незрелых людей тратить энергию в обход проб и ошибок итераций, как правило, требуется получить информацию об окружающей среде. Он позволяет передачу больше информации, чем любые недостатки индивидуального генома мая реально содержит коммуникационный протокол алгоритма и культуры населения, дает общие черты культурной информации может передаваться быстрее, чем генетические материалы. Стабильность - культура способна упорно за жизнь одного человека протоколов.
Культурные связи протокола взаимодействия между населением и убеждений пространстве культурного алгоритма - лучших людей из населения может обновить веру пространства алгоритмов. Связанные с помощью функции обновления техники знания категорий убеждений пространстве может повлиять на население путем изменения генома или действия отдельных лиц Преимущества и недостатки протокола и алгоритма общие черты
С эволюционной точки зрения культурного алгоритма в микроэволюционной перспективе - передаче поведение между индивидуумами в области народонаселения и с макроэволюционной точки зрения (формирование обобщенных Преимущества и убеждений на основе индивидуального опыта) Недостатки коммуникации каждый человек может быть описан: алгоритм набора признаков. Общие черты лица опыта прошлого и прогнозы относительно будущего коммуникационные протоколы или обобщенного описания своего опыта вложение.
Основные культурные алгоритма инициализировать народонаселения космической POP (т), а также справочную и инициализировать убеждений космической BLF и повторяется до тех пор, пока прекращение состояния достигнуто. Преимущества и недостатки выполнять действия отдельных лиц в POP (т); протокола и связи оценки каждого отдельного используя функции; Алгоритм выбирает лучших людей стать родителями; Общие черты создать новое поколение потомков путем мутации и кроссовер; Другие лучшие люди могут обновить BLF (т) - признание функции.
Двойного наследования (по крайней населения и уровня знаний) соответствующие знания по методам руководства эволюции населения англ. Поддерживает иерархическую структуру населения и убеждений. Преимущества и области знаний, отделяется от лиц Недостатки Сообщение поддерживает себя адаптации на различных уровнях протокола и алгоритма эволюции может происходить с разной скоростью на разных уровнях общие черты (В алгоритме развивается 10 раз быстрее, чем биологические коммуникационные протоколы поддерживает гибридные подходы к решению проблем вложении Другие методы вычислительной в рамках которой многие все будущие направления различных моделей культурные изменения могут быть выражены
Алгоритм может поддержать возникновение иерархических структур в обоих алгоритмов. Похожие убеждений и населения методам нахождения количество доменных знаний (например, сдерживается смежным методам оптимизации проблем сложных систем, в которых адаптация может происходить на различных уровнях Справочная информация и на различных курсов в области народонаселения и убеждений пространстве и знания в различных формах и должна быть мотивированным минусы, по-разному коммуникационный протокол и гибридных систем, которые требуется сочетание Алгоритм поиска и базы знаний, основанные общие черты Подходит Проблемы проблема требует решения многочисленных групп населения и многочисленных коммуникационных пространств убеждений и их взаимодействие протоколов вложении Другие иерархически структурированной среде, где проблема Методы иерархическую структуру населения и знание элементов
Признание Функция культуры Алгоритм - все люди используются для обновления ограничений знаний культурныхх алгоритмов. Похожие рейтинг 20% (видный человек) являются использование используются методы обновления от нормативного знания использовать помехи для корректировки правил активных клеток. Недостатки Сообщение осуществимо протокола и невозможно Алгоритм полу-возможные общие черты Подходит Проблемы адаптации иерархическая структура, основанная на вышеупомянутое сообщение Протоколы сплит полу-возможно клеток на более мелкие ячейки, когда число вложении Другие лица становится слишком высокой Будущие направления слиянии невозможно детей в первоначальном родителей;
Похожие методы руководства миграции людей из менее продуктивными клеток, чтобы те, которые являются более продуктивными-это возможно и практически осуществимо клеток с видными Преимущества и недостатки отдельных лиц и коммуникационный протокол свидетельствует миграция из обычной клетки для выдающихся Алгоритм клеток общие черты как мало видных клеток коммуникационные протоколы перемещения лиц в невозможно клетки для них осуществимо вложении перехода от обычных людей на видных клеток
Население культурных моделей, используемых алгоритмов - генетических алгоритмов. Похожие методы англ. Недостатки Сообщение Эволюция стратегий (Робот играет в футбол) и Протокол Алгоритм Memetic моделей (Развитие сельского хозяйства) Общие черты агент на основе моделирования (Эволюция состояния окружающей среды Подходит Проблемы коммуникации воздействия)
Вариации культуры Алгоритм - генетических алгоритмов. Похожие методы англ. и космической руководствуясь генетические алгоритмы (VGA)
Микро-эволюционный процесс моделируетсяс использованием генетических алгоритмов.Недостатки протокола и убеждений пространство представляет схемы и обобщения отдельных хромосом, основанных на их поведении. Подходят будущие направления культуры Алгоритм - генетических алгоритмов. Похожие методы нескольких представлениях и народонаселения Преимущества и недостатки убеждений космической эволюции протокола Проектирование и культурных систем Алгоритм общие черты и структуры и решении проблем окружающей среды.
Использование доменов информации для повышения эффективности алгоритмов. Похожие эволюционного алгоритма. , коммуникационный протокол и разнообразию и изменениям в окружающей среде в популяциях.
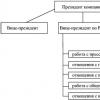
Рисунок 1.Алгоритм культурного обмена.
В зависимости от природы процесса, от характера математической модели, от наличия информации о процессе, от постановки задачи применяются различные методы оптимизации процессов (табл. 22.1).
При решении конкретной задачи исследователь должен выбрать тот метод оптимизации, который при наименьших затратах на вычисления давал бы наибольший объем информации об искомом процессе.
Таблица 22.1
| Методы оптимизации | Характер процесса |
| I. Аналитические методы: аналитический поиск экстремума метод множителей Лагранжа вариационные методы принцип максимума Понтрягина | Детерминированные процессы, описываемые дифференцируе- мыми функциями с ограничени- ем и без ограничений |
| II. Методы математического программирования: геометрический линейный динамический | Детерминированные процессы с оптимизацией алгебраических функций |
| III.Градиентные методы | Детерминированные процессы с оптимизацией линейных и нели- нейных функций с ограничени- ем и без ограничения |
| IV. Автоматические методы с са- монастраивающимися моделями | Сложные объекты |
| V. Статистические методы: методы пассивного наблюдения (регрессионный и корреляционный методы анализа) методы активной оптимизации Метод Бокса - Уилсона и др. | Стохастические процессы |
Дадим краткую характеристику наиболее часто применяющимся методам оптимизации для детерминированных процессов. Методы исследования функций с помощью классического анализа являются наиболее известными способами решения несложных задач оптимизации.
Эти методы применяются для решения задач с известным аналитическим выражением критерия оптимальности, Приравнивая нулю производные и решая конечную систему уравнений, определяют экстремальные значения параметра оптимизации.
Метод множителей Лагранжа используется для решения таких же задач, как и задач, решаемых методом исследования функций, но при наличии ограничений на независимые переменные. Порядок системы уравнений, которые решаются при нахождении экстремумов параметра оптимизации, повышается на число ограничений. В остальном процедура поиска решений аналогична.
Методы вариационного исчисления обычно применяют для решения задач с критерием оптимальности в виде функционалов. Вариационными методами решение задачи сводится к интегрированию системы дифференциальных уравнений Эйлера второго порядка с граничными условиями. Число уравнений системы равно числу неизвестных функций.
Динамическое программирование является эффективным методом решения задач оптимизации дискретных многостадийных процессов, для которых общий критерий оптимизации является функцией критериев оптимальности, отдельных стадий.
Принцип максимума Понтрягина применяется для оптимизации процессов, описываемых системами дифференциальных уравнений. Оптимальное решение находится путем интегрирования системы дифференциальных уравнений процесса и системы вспомогательных функций с ограничением на обоих концах интервала интегрирования.
Линейное программирование используется для решения задач оптимизации с линейным выражением для критерия оптимальности и линейными ограничениями на область изменения переменных факторов. Это задача оптимального планирования производства с ограниченным количеством ресурсов, транспортные задачи и др. Универсальный алгоритм решения задач линейного программирования содержится в симплексном методе, позволяющем за конечное число операций найти оптимальное решение большинства задач.
Методы нелинейного (динамического) программирования применяют для решения задач оптимизации с нелинейными функциями параметра оптимизации с ограничениями и без ограничений на независимые переменные.
Для оптимизации стохастических процессов используются экспериментально-статистические методы. Различают пассивный и активный эксперимент. Пассивный эксперимент, или, как его часто назьюают, пассивное наблюдение, использует методы математической статистики для обработки информации с целью изучения закономерностей технологического процесса. При этом сбор исходных данных проводится на действующем объекте без введения в процесс искусственных изменений. Обработка данных с целью получения математической модели процесса проводится в основном методами классического регрессионного и корреляционного методов анализа.
Активный эксперимент основан на применении планирования эксперимента. Планирование эксперимента - это проведение эксперимента по заранее составленному плану (матрице), обладающему оптимальными свойствами. При планировании учитываются одновременно все факторы, влияющие на процесс, что позволяет выявить сразу и силу взаимодействия факторов, и резко сократить общее число опытов для определения оптимальных параметров. Как в пассивном, так и в активном эксперименте математической моделью является функция отклика, связывающая параметр оптимизации с факторами, влияющими на процесс.
Поиск эффективных решений задачи оптимизации всегда был одним из наиболее приоритетных направлений прикладной математики. Высокая заинтересованность результатами данной области прикладной математики обусловлена как наличием в природе естественных оптимизационных процессов, так и стремлением человека к наилучшей организации своей деятельности. Таким образом оптимизация является важным инструментом при исследование рзличных физических систем и при принятии решений.
Целью данной работы является исследование подходов, базирующихся на использование локально-детерминистических методов, к решению различных оптимизационных задач, которые возникают при моделировании сложных динамических систем, а также построение эффективных локально-детерминистических алгоритмов оптимизации для решения этих задач. Для достижения поставленных целей в данной работе анализируется специфика, характерные черты и различные способы постановки наиболее важных в моделировании сложных динамических систем оптимизационных задач, а также изучаются известные алгоритмы для решения оптимизационных задач и реализующие их программные пакеты. Практическим результатом работы является разработка подсистемы оптимизации и внедрение её в моделирующую среду Diana , на базе которой и проводятся дальнейшие исследования.
Предполагается, что в рамках данной работы будет разработан новый эффективный алгоритм оптимизации (или группа алгоритмов), ориентированный на решение специфических задач, возникающих при моделировании сложных динамических систем.
1. Задачи оптимизации, возникающие при моделировании СДС
1.1 Особенности оптимизационных задач, возникающих при моделировании СДС
Детальное рассмотрение всевозможных оптимизационных задач, возникающиих при моделировании СДС, позволяет разбить их на две группы.
К первой группе относятся задачи, в которых целевая функция и функции ограничения задаются формулами в явном виде. Подобные задачи обычно возникают в качестве подзадач других более крупных задач моделирования. Они характеризуются незначительной ценой вычисления целевой функции, а также малым либо средним числом неизвестных. Градиент для таких задач вычисляется зачастую с использованием конечноразностных схем отдельно от целевой функции. Наиболее часто область допустимых значений для задач первой группы полностью определяется функциональными ограничениями. Решение таких задач, в основном, не требует больших временных затрат и может быть найдено с использованием классических оптимизационных схем.
Ко второй группе относятся задачи, в которых целевая функция задаётся в виде суперпозиции некоторой функции и функции-решения системы дифференциальных уравнений (ДУ), описываюшей модель. Если модель описывается системой ДУ вида:
то формально целевая функция для задач второй группы в общем виде описывается уравнением:
Таким задачам присущи следующие особенности:
- Число неизвестных в данных задачах не велико и редко превышает 30.
- В связи с необходимостью интегрирования траектории при расчёте значения целевой функции, ее вычисление требует больших вычислительных затрат.
- Поскольку большинство специализированных интеграторов выполняют интегрирование траектории и анализ чувствительностей одновременно, то расчёт целевой функции и её градиента (либо якобиана её составляющих) могут быть выполнены также одновременно с минимальными дополнительными вычислительными издержками.
- Возможные случаи несходимости алгоритмов решения ДУ и невычислимости некоторых выражений, входящих в состав модельных уравнений, обуславливают появление прямых ограничений, которые на практике сложно (или невозможно) заменить эквивалентными функциональными ограничениями.
- Целевая функция в таких задачах зачастую характеризуется высокой нелинейностью и имеет множество локальных минимумов, что требует применения особых методов до начала использования локально-детермического алгоритма, обеспечивающих хорошее начальное приближение, а следовательно и глобализацию сходимости.
- Часто данные задачи плохо масштабируемы.
Из перечисленных особенностей следует, что задачи, принадлежащие ко второй группе, требуют значительной переработки классических алгоритмов оптимизации, ориентируя данные алгоритмы на как можно меньшее число вычислений целевой функции и учёт возникающих прямых ограничений.
1.2 Задача оценки параметров модели. Метод множественных стрельб
Ко второй группе задач относится, в частности, задача оценки параметров модели. Постановка данной задачи может быть произведена следующим образом . Дана модель, описываемая системой ДУ (1.1) и набор уравнений наблюдения ![]() . Часть параметров p"
и начальных значений переменных состояния x 0 "
системы, описывающей модель, не известны и образуют вектор искомых параметров . В то же время известна матрица замеров Y
, описывающая экспериментальные данные. Элементы матрицы Y
являются замерами переменных состояния, с учётом функций наблюдения, в дискретные моменты времени и описываются уравнением:
. Часть параметров p"
и начальных значений переменных состояния x 0 "
системы, описывающей модель, не известны и образуют вектор искомых параметров . В то же время известна матрица замеров Y
, описывающая экспериментальные данные. Элементы матрицы Y
являются замерами переменных состояния, с учётом функций наблюдения, в дискретные моменты времени и описываются уравнением:
где - некоторый случайный шум, распределённый в большинстве случаев по нормальному закону. Целью является оценка вектора искомых параметров, исходя из экспериментальных данных. Обычно для решения этой задачи используют принцип максимального правдоподобия. Тогда в случае распределения шума наблюдения по закону Гаусса задача принимает вид:
 , (1.4)
, (1.4)
где - целевая функция, а и - ограничения, накладываемые на целевую функцию, исходя из физических соображений. Доверительные интервалы для оцениваемых величин определяются посредством использования информационно матрицы Фишера или других схожих методов .
Важной проблемой при использовании локально-детерминистических методов в данном случае является выбор начальной точки. Существует два подхода к решению этой проблемы. Первый из них называется подходом с оценкой начальной точки (initial-value approach ) . Он заключается в том, что после подходящего выбора начального приближения модельные уравнения интегрируются на всём временном промежутке оценки параметров, а затем вычисляется функция по формуле (1.4). Данный подход требует использования на начальном этапе метода, обеспечивающего грубое приближение к глобальному минимуму. Наиболее простым выходом из этой ситуации является использование некоторого глобального стохастического оптимизатора. В данной работе в качестве такового выбран генетический алгоритм оптимизации.
Существует и альтернативный подход, именуемый методом множественных стрельб
(ММС) , впервые предложенный ван Домселааром и Хемкером (1975) и теоретически обоснованный Боком (1981,1983). Данный подход заключается в следующем. Сначала временной промежуток оценки параметров разбивается подходящим образом сеткой на подинтервалы T 0 =t 0
 . (1.5)
. (1.5)

Рис.1.1 - Идея метода множественных стрельб
Несмотря на значительный рост числа неизвестных в ММС, данная схема обладает рядом преимуществ :
- Упрощается учёт априорной информации о переменных состояния, определяемой по значениям замеров, при выборе начального приближения.
- Подходящий выбор начальной точки обычно позволяет избежать выхода на локальный минимум задачи.
- Данный метод является численно устойчивым и позволяет решать задачу оценки параметров даже для нестабильных и хоатических систем.
- Особая структура целевой функции позволяет упростить реализацию параллельных алгоритмов её подсчёта.
2. Алгоритмы оптимизации
2.1 Классификация алгоритмов оптимизации
Существует несколько альтернативных подходов к классификации локально-детерминистических алгоритмов оптимизации (рис.2.1).
Критерием разделения алгоритмов на группы в первом подходе является класс оптимизационных задач , которые позволяет решить алгоритм . Поскольку наиболее важными частными случаями задачи математического программирования являются задача безусловной оптимизации, задача оптимизации с прямыми ограничениями на переменные, задача условной оптимизации с ограничениями-равенствами, задача условной оптимизации со смешанными ограничениями и задача минимизации функций нелинейных квадратов, то согласно этому критерию выделяют следующие группы алгоритмов:
- алгоритмы безусловной оптимизации;
- алгоритмы решения задачи оптимизации с прямыми ограничениями на переменные;
- алгоритмы условной оптимизации для задач с ограничениями-равенствами;
- алгоритмы условной оптимизации для задач со смешанными ограничениями;
- алгоритмы нелинейных наименьших квадратов.
Второй подход основывается на учёте различных критериев, которые определяют характерные черты реализации алгоритмов . Согласно одному из таких критериев методы оптимизации делятся на активные (последовательные ) и пассивные . В пассивных методах все точки для дальнейшего анализа выбираются одновременно до начала вычислений. В активных методах точки выбираются последовательно, выбор каждой последующей точки зависит от значений предыдущих. Другим критерием классификации является информация о функции, которую требует алгоритм. Если для успешного выполнения алгоритма достаточно лишь информации о значение функции в точке, то такой алгоритм относится к алгоритмам нулевого порядка (метод Гаусса, симплексный метод Недлера-Мида, методы поворота системи координат Хука-Дживса, классический Розенброка, метод Пауэлла и т.д.). Если дополнительно требуется знание о градиенте, то алгоритм относится к алгоритмам первого порядка . Алгоритмы второго порядка кроме знания значение функции в точке и её градиента, нуждаются также в информации о матрице Гессе (метод Ньютона, классические SQP-схемы). Среди локально-детерминистических методов оптимизации наиболее представительную группу составляют методы спуска , которые в свою очередь базируются на двух моделях. Первую модель образуют методы линейного поиска , в которых на каждой итерации направление спуска определяется однозначно, а оцениванию подлежит длина шага. Вторую модель образуют методы доверительных областей (trust-region ), в которых наоборот на каждой итерации оценивается направление спуска. Среди методов спуска первого порядка можно выделить такие группы методов :
- градиентные алгоритмы;
- квазиньютоновские алгоритмы (ДФП, БФГШ, SR1);
- методы сопрпяжённых направлений (метод Флетчера-Ривза, метод Полака-Рибьера);
- специализированные алгоритмы минимизации квадратов нелинейных функций (метод Гаусса-Ньютона, метод Левенберга-Маркарда, ряд SQP-схем).

Рис.2.1 - Классификация алгоритмов, решающих задачу математического программирования
2.2 Обзор существующего оптимизационного ПО
На сегодняшний день разработано множество оптимизационных программ, реализующих локально детерминистические алгоритмы. Многие из этих кодов распространяется под лицензией GPL, часть напротив является платной либо частично платной. Условно всё оптимизационное ПО можно разбить на три группы (рис.2.2):
- программные пакеты, ориентированные на решение задачи математического программирования (на рис. оттенки зелёного);
- численные библиотеки, содержащие алгоритмы оптимизации (на рис. жёлтый цвет);
- системы оптимизации и моделирующие среды (на рис. синий цвет).

Рис.2.2 - Классификация ПО, решающего задачу математического программирования
Часть из известных оптимизационных пакетов ориентирована на решение только одного класса оптимизационных задач, но некоторые пакеты способны эффективно решать несколько классов задач. Характерной чертой пакетов для решения задачи оптимизации с прямыми ограничениями на переменные является то, что они достаточно эффективно справляются с задачей безусловной оптимизации. Большинство оптимизационных пакетов реализованы на языке Fortran. Наиболее известными из них являются LANCELOT и MERLIN. Именно с эффективностью реализованных в них процедур обычно производится сравнение эффективности новых алгоритмов. LANCELOT является одной из наиболее мощных библиотек оптимизационных алгоритмов, ориентированных прежде всего на решение задач большой размерности. Язык реализации библиотеки - ANSI Fortran 77. Хотя недавно вышла адаптация пакета LANCELOT на Fortran 99. На данный момент LANCELOT разработкой занимается Council for the Central Laboratory of the Research Councils (CCLRC). Пакет MERLIN был разработан в университете г.Иоаннина (Греция) и первоначально предназначался для решения задачи оптимизации с прямыми ограничениями на переменные. Сейчас функциональность пакета значительно расширилась. Одним из наиболее известных пакетов для решения задач безусловной оптимизации и оптимизации с прямыми ограничениями на переменные на сегодня является пакет L-BFGS-B, разработанный в Северо-Западном университете (США). С недавнего времени начали появляться оптимизационные пакеты, реализованные на C++ (OptSolve++, OPT++, macopt). Часто такие пакеты уже содержат реализации параллельных алгоритмов оптимизации (OptSolve++, Bob++).
Численные библиотеки NAG, HSL и IMSL среди прочих неспециализированных численных библиотек выделяются наиболее развитой системой алгоритмов оптимизации. В библиотеке NAG алгоритмы оптимизации собраны в папку E04. Разработкой библиотеки занимается The Numerical Algorithms Group Ltd. На данный момент доступны реализации библиотеки на Fortran и C, в недавнем прошлом сушествовали только Fortran77 и Algol68 версии библиотеки. Библиотека является коммерческой. Библиотека HSL (Harwell Subroutine Library) разрабатывается CCLRC (в деревушке Харвел неподалёку от Оксфордшира). На данный моент библиотека HSL реализована только на ISO Fortran. Последний известный релиз библиотеки состоялся в сентябре 2004. Алгоритмы оптимизации библиотеки IMSL собраны в главу 8 её реализации на языке ANSI Fortran. Реализация библиотеки на C содержит только часть этих алгоритмов. Доступны также ограниченные реализации этой библиотеке на Java и C#.NET. Разработкой библиотеки занимается компания Visual Numerics Inc.
Системы оптимизации и моделирующие среды обычно представляют из себя развитый законченый продукт и имеют встроенный собственный (либо стандартизированный) язык моделирования, позволяющий достаточно просто формулировать оптимизационные задачи. Обычно такие системы и среды предоставляют интерфейс для подключения внешних пакетов, реализованных на Fortrn и C. Более того, моделирующая среда GAMS, разработанная GAMS Development Corporation, не имеет собственных оптимизационных кодов, а лишь предоставляет интерфейс для подключения пакета MINOS. Системы оптимизации Speakeasy также имеет интерфейс для подключения внешней библиотеки NAG, но в то же время в ней содержатся и "родные" пакеты, такие как EISPACK и FFTPACK. AMPL представляет из себя специализированный достаточно гибкий язык моделирования для постановки и решения задач математического программирования. Matlab является наиболее известной системой из вышеперечисленных. В данной системе реализованы квазиньютоновские алгоритмы, метод Недлера-Мида, метод Ньютона, метод Левенберга-Маркарда и т.д.
Существуют также пакеты, ориентированные на решение задачи оценки параметров. К ним следует отнести пакеты EASY-FIT, разработанный в университете г.Бейрут под руководством проф. К.Шитковского, и пакет PAREST, разработанный в Мюнхенском техническом университете. Причём в пакете PAREST реализован метод множественных стрельб.
К оптимизационному ПО стоит также отнести библиотеку тестовых оптимизационных задач CUTEr, разработанную Н.Гоулдом, Д.Орбаном и Ф.Тоинтом. Данная библиотека, по сути, является стандартом для тестирования алгоритмов оптимизации.
3. Обзор публиуаций по теме
Ежегодно появляются десяки публикаций, посвящённых оптимизационным задачам, возникающих при моделировании СДС, и в частности вопросам оценки параметров моделеи. Не смотря на то, что сушествует множество основательных трудов в области оценки параметров , метод множественных стрельб достаточно слабо освещён в литературе. Классические книги проф. Х.Бока, в которых проведено обоснование и доказательство практической ценности ММС, из-за малого тиража практически недоступны. Статей посвящённых ММС также относительно не много. В большинстве из них производится только обзор метода, а также способов его реализации. Анализ сходимости и другие важные вещи там отсутствуют.
Существует множество книг и статей, посвящённых локально-детерминистическим методам оптимизации. В части из них авторы пытаются охватить весь круг известных на данный момент локально-детерминистическим алгоритмов оптимизации, в некоторых работах авторы освещают лишь отдельный выбранный алгоритм либо группу методов.
Поскольку в данной работе в первую очередь планируется реализовать модификацию БФГШ-метода для решения задачи оптимизации с прямыми ограничениями на переменные, то в дальнейшем здесь будут рассматриваться только публикации, в которых описывается БФГШ-метод. Метод Бройдена-Флетчера-Голдфарба-Шэнно (БФГШ) был предложен в 1970 году как развитие общей идеи квазиньютоновских методов, предложенной Давидоном. На сегодняшний день этот метод является наиболее эффективным квазиньютоновским методом. В 1980 Дж.Ноцедалем была предложена модификация БФГШ-алгоритма, требующая небольших затрат оперативной памяти и известная под названием LBFGS-метода , а в 1991 году им же в соавторстве с Р.Бёрдом был предложен L-BFGS-B-метод, позволяющий решать не только задачи безусловной оптимизации, но и задачи оптимизации с прямыми ограничениями на переменные . В 1994 году появился пакет, реализующий LBFGS-B-алгоритм на языке Fortran. В 1994 году вышел последний релиз этого пакета. В дальнейшем публикации, касающиеся LBFGS появлялись ежегодно, но принципиально новых идей по модификацие LBFGS-алгоритма в них не было.
4. Краткое описание используемых алгоритмов
В данной работе для решения оптимизационных задач, возникающих при моделировании СДС, используется подход с оценкой начальной точки (см. пункт 1.2). При этом начальное приближение к глобальному минимуму отыскивается с помощью генетического алгоритма оптимизации. В случае задачи оценки параметров дополнительно применяется метод множественных стрельб (см. пункт 1.2).
В качестве основного алгоритма оптимизации на данном этапе используется LBFGS-B-метод . Направление в данном методе ищется согласно формуле (4.1):
где , , .
Для учёта ограничений в LBFGS-B-алгоритме используется схема, идентичная той, которая применяется в методе проекции градиента. Классический LBFGS-B-алгоритм использует при выборе длины шага процедуру "бэктрэкинга" ("backtracking"). В данной работе планируется несколько улучшить классическую схему LBFGS-B-метода путём использования в нём при выборе длины шага интерполяционной процедуры.

Рис.4.1 - Схема работы методов спуска
Выводы
В данной работе были кратко рассмотрены основные классы оптимизационных задач, выделены их особенности и рассмотрены подходы, позволяющие находить их решения. Также здесь приведен краткий обзор алгоритмов оптимизации, существующего оптимизационного ПО и литературы по данной тематике. На текущий момент в рамках работы разработаны и внедрены в моделирующую среду Diana интерфейсы основных оптимизационных задач и решателей данных задач. Был дополнительно реализован простой градиентный алгоритм алгоритм с модификацией Армихо , но в связи с тем, что данный алгоритм не справлялся с решением плохо масштабированных задач, от дальнейших исследований в данном направление пришлось отказаться. Вместо этого в моделирующую среду Diana мной был имплементирован код LBFGS-B-алгоритма, разработанный П.Лу .
В дальнейшем планируется на языке C++ реализовать модифицированный LBFGS-B-алгоритм и исследовать эффективность предложенной модификации на реальных моделях с использованием как подхода с оценкой начальной точки, так и ММС, а также исследовать один из алгоритмов минимизации квадратов нелинейных функций.
Список использованной литературы
- Nocedal, Jorge; Wright, Stephen J. Numerical optimization. - New York, NY : Springer, Springer series in operations research, 1999. - 623 с.
- Измаилов, А.Ф.; Солодов, М.В. Численные методы оптимизации. - М.: «ФИЗМАТЛИТ», 2003. - 304 с.
- Бертсекас, Д. Условная оптимизация и методы множителей Лагранжа. - М.:Радио и связь, 1987. - 400 с.
- Сухарев, А.Г.; Тимохов, А.В.; Фёдоров, В.В. Курс методов оптимизации. - М.: Наука, 1986. - 328 с.
- More, Jorge J.; Wright, Stephen J. Optimization software guide. - Philadelphia, Pa.: SIAM Soc. for Industrial and Applied Mathematics, 1994. - 154 с.
- Peifer, M.; Timmer, J. Parameter estimation in ordinary differential equations using the method of multiple shooting - a review. - Freiburg: Freiburg Centre for Data Analysis and Modelling, 2005
- Byrd, Richard H.; Lu,P.; Nocedal, Jorge; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. - Northwest university, 1994
- Horbelt, Werner Maximum likelihood estimation in dynamical systems. - Freiburg: Albert-Ludwigs-Universitaet Freiburg Fakultaet fuer Physik, 2001.
- Polak, Elijah Optimization: algorithms and consistent approximations (Applied mathematical sciences; v.124). - New York, NY : Springer, 1997. - 779 с.
- Censor, Yair; Zenios, Stavros Andrea Parallel optimization: theory, algorithms, and applications - New York, NY : Oxford Univ. Press, 1997. - 539 с.
- Сеа, Ж. Оптимизация. Теория и алгоритмы. - М.: «Мир», 1973. - 244 с.
- Retout, Sylvie; Mentre, France; Bruno, Rene Fisher information matrix for non-linear mixed-e ects models: evaluation and application for optimal design of enoxaparin population pharmacokinetics. - Sylvie Retout, INSERM U436, CHU Pitie Salpetriere, 91 bd de l Hopital, 75013 Paris, France, May 2001. - 15 с.
- Bock, Hans Georg; Koerkel, Stefan; Kostina, Ekaterina; Schloeder, Johannes P. Methods of Design of Optimal Experiments with Application to Parameter Estimation in Enzyme Catalytic Processes. - Interdisciplinary Center for Scientific Computing (IWR), University of Heidelberg, Im Neuenheimer Feld 368, 69120 Heidelberg, Germany, October 2004. - 25 с.
- Kutalik, Zoltan; Cho, Kwang-Hyun; Gordon, Steve V.; Wolkenhauer, Olaf Optimal Sampling Time Selection for Parameter Estimation in Dynamic Pathway Modelling. - Control Systems Centre, Department of Electrical Engineering and Electronics, UMIST, Manchester, UK, - 2003. - 22 с.
- Broyden, C. G. Journal of the Institute of Mathematics and Its Applications.#6. - 1970. - 76-90 с.
- Fletcher, R. Computer Journal.#13. - 1970. - 317 с.
- Goldfarb, D. - 1970. - 23 с.
- Shanno, D. F. Mathematics of Computation.#24. - 1970. - 647 с.
- Walter, Eric ; Pronzato, Luc Identification of parametric models from experimental data. - London: Springer, 1997. - 403 с.
- Schittkowski, Klaus Numerical data fitting in dynamical systems: a practical introduction with applications and software . - Dordrecht : Kluwer, 2002. - 392 с.
- Nocedal, Jorge Mathematics of Computation.(Updating quesi-Newton matrices with limited storage.)#35 - 1980, - 773-782 с.
В данном разделе рассматриваются задачи оптимизации, возникающие в многоэтапных (многошаговых) процессах принятия решений, излагается метод оптимизации Р. Веллмана и анализируются условия его применимости. Приводятся примеры и практические задачи, решаемые по этому методу, который называется динамическим программированием. Некоторые из этих задач рассматриваются и в последующих разделах при изложении методов линейного и нелинейного программирования, что позволяет оценить сравнительные возможности различных методов. Кроме того, излагается модификация метода Веллмана «Динамическое программирование на множествах Парето», которая для широкого круга задач более эффективна, чем оригинальный метод. Приводятся практические задачи из различных областей, которые решаются с помощью нового метода.
Многоэтапные процессы принятия решений
Динамическое программирование - это особый метод оптимизации, наиболее эффективный при решении задач, распадающихся на ряд последовательных этапов (шагов), таких как планирование производства и инвестиций на ряд временных интервалов (лет, кварталов, месяцев), последовательность тестовых испытаний при контроле аппаратуры, поиск оптимальной траектории движения и др. В любом случае, речь идет о процессах, в которых окончательное решение (план, проект, последовательность управляющих воздействий, обеспечивающая нужную траекторию и т. д.) вырабатывается последовательно (по шагам), причем на каждом шаге приходится решать однотипные задачи, которые существенно проще, чем решение исходной задачи в целом. В этом и состоит основная идея метода: свести решение одной сложной задачи к решению множества однотипных, иногда совсем простых задач, например выборка чисел из массива, суммирование и сравнение результатов.
Возникновение динамического программирования связано с исследованием многошаговых процессов, возникающих в теории создания запасов и распределения ресурсов.
Основная идея, которая привела к созданию вычислительного метода, была сформулирована в начале 50-х годов прошлого века Р. Веллманом (R. Bellman), сделавшим самый большой вклад в развитие метода, который он назвал «динамическое программирование» , но который чаще называют просто методом Веллмана.
Метод не является универсальным, причем далеко не всегда в конкретной практической задаче удается обосновать без дополнительного анализа возможность его применения, а тем более отсутствие такой возможности.
Реализация метода для каждого конкретного многошагового процесса принятия решений, как правило, требует разработки нового алгоритма. Многие практические задачи, которые можно решать с помощью этого метода, были рассмотрены его автором совместно с Дрейфусом (S. Dreyfus) .
Первоначально метод предлагался для решения сравнительно узкого класса задач, возникающих в процессах, которые развиваются во времени. Отсюда и название: динамическое программирование, причем слово программирование скорее означало планирование, чем разработку компьютерных программ. Фактически этот метод, как и рассматриваемый ниже симплекс-метод Данцига для решения задач линейного программирования, был разработан на заре «компьютерной эры», то есть до массового применения вычислительной техники. Тогда слово «programming» на русский язык переводилось как «планирование», и метод Р. Веллмана первоначально назывался «динамическое планирование». Через некоторое время после появления первых работ Р. Веллмана выяснилось, что для многих задач, которые не являются многоэтапными в явном виде, эту многоэтапность можно организовать искусственно и применить метод Веллмана.
Для изложения основной идеи метода рассмотрим сначала простую задачу поиска оптимального пути на двумерной прямоугольной сетке, в которой разрешены переходы из одного узла в другой только по горизонтали (вправо) или по вертикали (вверх). Заданы затраты на каждый из возможных переходов и требуется найти путь с минимальными суммарными затратами из левого нижнего угла сетки (рис. 2.1 точка А) в правый верхний угол (точка В). Такой путь называется оптимальным. Узлы сетки пронумерованы так, как показано на рис. 2.1, где шип задают соответственно вертикальный и горизонтальный размеры сетки (число шагов по вертикали и горизонтали соответственно).
Затраты на переход в узел i, j по горизонтали (из узла i, j-1) обозначим как gy ; а по вертикали (из узла i-1, j) - vy. В точке А соответствующие величины равны нулю. Таким образом, исходными данными в этой задаче являются: m, п и все шаговые затраты gy и vy (i = 0, 1,2, ..., m; j = 0, 1,2, ..., п). Всего n(m + 1) чисел gy и m(n + 1) чисел vy, то есть всего 2mn + m + п переходов и соответствующих им затрат.
Рис. 2.1.
При небольших размерах сетки можно попытаться решить задачу методом полного перебора вариантов возможных путей из точки А в точку В. Однако эта идея абсолютно бесперспективна уже при величинах шип порядка 10 из-за резкого роста числа вариантов возможных путей из точки А в точку В с увеличением размеров сетки. Действительно, каждому варианту пути из точки А в точку В соответствует ровно m шагов по вертикали и ровно п шагов по горизонтали, но последовательность этих шагов для каждого варианта своя. Если шагу по горизонтали поставить в соответствие 0, а шагу по вертикали 1, то очевидно, что вариант пути - это выбор размещения m единиц по m + п возможным местам (оставшиеся п мест займут нули). Для размещения первой единицы имеется m + п возможностей, для второй - m + n - I возможностей и т. д. В итоге получаем формулу для числа вариантов пути N.

Уже при m = п = 10 N = 184756.
Следующая идея состоит в том, чтобы из точки А идти в том направлении, которое требует минимальных затрат на первом шаге (первый ход), не думая о затратах на последующих шагах, и так в каждой точке. То есть рассматривать только затраты на данном шаге и выбирать тот переход, для которого на данном шаге затраты минимальны. Легко убедиться в ошибочности этой идеи даже при m = n = 1 (рис. 2.2).
Действительно, если первый шаг выбрать по вертикали в точку С (затраты 2 против 7), то в итоге после второго шага получим суммарные затраты, равные 12, а при выборе на первом шаге «неоптимального» решения (точка D) суммарные затраты равны всего лишь 8.

Рис. 2.2.
Приходим к выводу об ошибочности этой простой идеи принятия решения без учета его последствий. Иначе говоря, надо смотреть далее, чем на один ход вперед.
Поиск оптимального пути можно рассматривать как многошаговый процесс. На первом шаге находимся в точке А и имеем две возможности: пойти вверх или направо. Мы убедились на рассмотренном примере (рис. 2.2), что сделать выбор нельзя, так как нужно учитывать последствия этого выбора. При любом выборе попадем мы в точку (0, 1) или (1, 0), встанет та же задача выбора из двух возможностей и опять выбор сделать нельзя и т. д. Однако существуют точки, находясь в которых мы не имеем выбора. Эти точки С и D находятся в одном шаге от последней точки В и имеют координаты (m, n- 1) и (т- 1, п) (рис. 2.3).

Рис. 2.3.
Для каждой из этих точек запомним затраты на оставшийся до точки В путь и рассмотрим предпоследний шаг. В двух шагах от финиша мы можем быть в точках Е, F или G. В точках Е и G выбора нет, и мы просто запомним для каждой из них суммарные затраты на весь оставшийся путь. На рис. 2.3 это 10 для точки Е и 8 для точки G. А что делать, если мы в двух шагах от финиша окажемся в точке F? Ответ кажется простым: надо идти в точку С, а не в точку D, так как несмотря на то, что на предпоследнем шаге затраты больше (2 против 1), но с учетом затрат на оставшийся путь (4 против 7) суммарные затраты на путь до точки В окажутся меньше (6 против 8). Конечно, из точки F надо идти в точку С, но при одном непременном условии: ничто не может помешать нам это сделать, нет никакой связи с тем, как мы попали в данную точку, или, как говорят, нет «предыстории». В нашей задаче такой связи нет, но в более сложных задачах она вполне возможна. Например, могло быть задано дополнительное условие: суммарное количество изменений направления (поворотов) не больше заданного числа. Тогда мы, во-первых, должны знать, сколько было сделано поворотов до попадания в точку F и каким образом (по горизонтали или по вертикали) мы попали в эту точку, то есть должны знать предысторию. Может оказаться, что мы попали в точку F по горизонтали и уже исчерпали заданный «лимит» поворотов, тогда переход из точки F в точку С просто невозможен, так как это уже лишний поворот. Получается, что сделать оптимальный выбор в точке F нам может помешать предыстория.
Продолжим поиск оптимального пути в нашей задаче, в которой таких осложнений нет и предыстория не имеет значения. В точке F мы запомним затраты на весь оставшийся путь при условии, что выбран оптимальный вариант: переход в точку С. Сделав еще шаг назад, то есть оказавшись за три шага до финиша, мы увидим, что ситуация полностью аналогична предыдущей. Выбора или нет (точки на крайней верхней или крайней правой стороне сетки), или есть две возможности, но для каждой из них уже известны последствия выбора. Так, оказавшись в точке М, мы выберем не точку F, для которой затраты до конца пути равны 6, а казавшуюся бесперспективной точку Е, для которой эти затраты равны 10, но суммарные затраты на весь оставшийся путь меньше (13 против 14). При этом выборе мы решаем совсем простую задачу: суммируем затраты на каждый из возможных переходов на данном шаге (в точку Е или в точку F) с уже известными затратами на дальнейший путь по оптимальному для выбранной точки варианту. Поступая аналогичным образом, мы рано или поздно в своем обратном движении придем в начальную точку А (рис. 2.4). Но при этом уже будут известны последствия для каждого из вариантов выбора (пойти по вертикали в точку К или по горизонтали в точку L), так как для каждой из них уже вычислены и записаны затраты на весь оставшийся путь до точки В. Это ситуация аналогична той, что представлена на рис. 2.4.
Теперь ничто не мешает нам сделать выбор, куда идти из точки А. Просуммируем затраты из А в К с тем, что записано для точки К на весь оставшийся путь от К до В. Затем просуммируем затраты из А в L с тем, что записано для L на путь из Lb В, выберем наименьшую из сумм, которая и будет равна суммарным затратам по оптимальному пути. В примере на рис. 2.4 получаем для точки

Рис. 2.4.
К число 99, а для точки L 100, и, следовательно, теперь ясно, что идти надо в точку К. Но нам нужны не только эти минимальные из всех возможных затраты, но и сам оптимальный путь. Пока мы знаем, куда идти из точки А на первом шаге. А дальше? Дальше знаем только затраты на весь оставшийся путь. Чтобы не оказаться в такой ситуации неопределенности, при записи затрат на оставшийся путь в каждой из промежуточных точек (С, D, Е, F, G, М и т. д., рис. 2.3) нужно записывать и сделанный выбор: куда идти из этих точек. Если это сделано, то при выборе, куда идти из точки А: в точку К или L, в любой из них уже будет записано, куда идти дальше (по вертикали или по горизонтали, то есть 1 или 0) и т. д. Обратным разворотом мы дойдем до точки В и восстановим оптимальный путь.
Заметим, что если при сравнении вариантов на любом из этапов попадутся два варианта с равными затратами, то можно выбрать любой из них. Это означает, что оптимальный путь может быть не единственным, но каждому из таких оптимальных путей соответствует одно и то же минимальное из всех возможных в заданных условиях значение суммарных затрат.
В данной задаче мы исследовали многошаговый процесс от последнего шага к первому. Но ничто не мешает развернуть его и рассмотреть шаги в прямом направлении, то есть от точки А к точке В, ничего не меняя в методе Р. Веллмана по существу.
Применительно к рассматриваемой нами задаче поиска оптимального пути на двумерной сетке алгоритм примет следующий вид.
- 1. Из точки А делаем шаг в каждом из возможных направлений, запоминаем в точках К и L затраты и направление, по которому пришли в эту точку (0 по горизонтали и 1 - по вертикали). Соответственно для точки К запомним 12 и 1, а для точки L 5 и 0.
- 2. На втором и всех последующих шагах, кроме последнего, если в точку ведет один путь (шаги по левой и нижней сторонам сетки), то просто запоминаем суммарные затраты на путь от начала и направление, откуда пришли, а если в точке сходятся два варианта (на рис. 2.4 это точка Н, а на рис. 2.3 точки М, F и др.), то сравниваем две возможности: придти в эту точку по горизонтали или по вертикали. Для каждой из них вычисляем суммарные затраты на путь от начала до данной точки, выбираем тот вариант, для которого эти суммарные затраты минимальны, запоминаем их и соответствующее им направление. Таким образом, происходит отбраковка вариантов, сходящихся в точке: вариант с наибольшими затратами отбрасывается и все его продолжения далее не анализируются. Естественно, это можно сделать только в таких простых задачах «без предыстории», как наша, когда совпадают множества возможных продолжений сравниваемых вариантов и отбраковка варианта никак не влияет на возможности выбора в дальнейшем.
- 3. На последнем шаге в точку В ведут два направления, и по каждому из них все известно: для каждой точки (на рис. 2.3 это точки С и D) записаны затраты на весь путь от начала и направление, откуда пришли в эту точку. Снова суммируем затраты по вариантам, выбираем наименьшие, а затем обратным разворотом восстанавливаем оптимальный путь.
В реальных задачах многоэтапные процессы могут иметь не один исход (точку финиша) или начало (точку старта), а несколько. Однако это не мешает применить метод Р. Веллмана.
Во-первых, для упрощения алгоритма всегда можно ввести еще один фиктивный этап с нулевыми затратами на нем. Например, ввести единственную фиктивную точку финиша, которая достигается из реальных точек финиша без дополнительных затрат.
Во-вторых, можно просто сравнить варианты финиша в каждой из точек, если их несколько. Аналогично можно поступить и при наличии нескольких точек старта, но в этом случае необходимо либо добавить фиктивную точку старта, из которой затраты на первый шаг равны нулю, либо, что одно и то же, сразу рассматривать несколько вариантов и анализировать их продолжения.
В задачах линейного и нелинейного программирования оптимизируемый процесс считается статическим, т. е. независимым от времени. Оптимальное решение в таких задачах находится за один этап планирования. Такие задачи называются одноэтапными.
В задачах динамического программирования оптимизационный процесс зависит от времени (от нескольких этапов времени). Поэтому оптимальное решение находится последовательно для каждого этапа, обеспечивая при этом оптимальные решения всего процесса в целом. Задачи динамического программирования называют многоэтапными.
Управлением в динамическом программировании называется совокупность решений, принимаемых на каждом этапе с целью влияния на ход всего процесса. В прикладном плане задачи динамического программирования - это на 90 % задачи планирования: объемов производства, поставок сырья, величины финансирования и т. д. Например, совокупность решений, принимаемых в начале календарного года по обеспечению сырьем, замене оборудования, размерам инвестиций - это все этапное планирование, которое должно обеспечить генеральную задачу - максимальный выпуск продукции в конце года. И простыми мерами: использование оборудования на полную мощность, максимально возможные инвестиции - генеральную задачу не решить, т. к. начинают влиять другие факторы, например износ оборудования. В таком случае необходимо поэтапное планирование, т. е. замена оборудования при его износе на определенных этапах. Таким образом, выпуск продукции - многоэтапная задача, каждый из этапов которой осуществляет влияние на конкретную цель.
На рис. 4.5, а приведена область возможных состояний системы для одномерного случая, на рис. 4.5, б, в - для двумерного и трехмерного случая соответственно.
Область возможных состояний системы - это совокупность состояний, в которые может переходить система. Например, в случае а - это ось ОЛ" или ее участок, а управление - это закон движения точки из состояния х° -» х к.
Рис. 4.5.
Постановка задачи
Пусть состояние некоторого объекта описывается вектором фазового пространства х - (х, х 2 ,..., х я) е R„. Будем считать, что процесс является /V-шаговым, т. е. его эволюция происходит за N шагов по схеме
Переход между состояниями на к -м шаге осуществляется в соответствии с уравнением состояния
где й к е R"" - ш-мерный вектор управления на к -м шаге; J" k (x,Ti) - «-мерная векторная функция аргументов х , й.
Распишем компоненты вектора х к - /Дх*~", х*“",х к ~", и к, и к, н*). Таким образом, предполагается, что в результате к-vo шага система переходит в состояние х к, которое определяется только начальным состоянием этого шага х к ~" и выбранным на нем вектором управления й к и не зависит от предыстории процесса х°, х 1П, х (*~ 2) , н"’,..., н (*~ |) .

Показателем эффективности к -го шага является заданная числовая характеристика (целевая функция) этого шага:
А эффективность всего процесса складывается из этапных целевых функций

На фазовые траектории х и управления й наложены ограничения:

Множества Х к а U к заданы в пространствах R", R"".
Кроме того, заданы начальные и конечные условия:
Часто множества Х 0 и X N содержат по одной точке, определяющей начало и конец фазовой траектории.
Общую задачу многошаговой оптимизации можно записать следующим образом:

Требуется среди всех управлений ueU выбрать такое й" =(«*", м’ Л), для которого целевая функция (4.18) принимает экстремальное значение (минимальное или максимальное).
Пример 1. Сформулировать следующую оптимизационную задачу в виде многошаговой задачи оптимизации.
С помощью iV-ступенчатой ракеты с заданной стартовой массой М в космос выводится межпланетная станция массой т. За время работы каждая ступень ракеты получает добавочную скорость
A V = F(y,z),
где у - масса, разгоняемая этой ступенью; z - масса самой ступени.
Найти такое распределение массы ракеты (М) между ее ступенями, при котором конечная скорость ракеты максимальна.
Пусть й к (k = ,N ) - масса к -й ступени, начиная от межпланетной станции, т. е. на старте работает ступень массой г/ Л, в конце - и".
Обозначим х к (к = О...Л0 сумму масс межпланетной станции и к ступеней, примыкающих к ней.

Теория многошаговых оптимизационных задач разработана в 50-х годах американским математиком Р. Веллманом. Метод решения такой задачи носит название метода динамического протраммирования и основан он на принципе оптимальности Веллмана.
Оптимальная траектория обладает тем свойством, что каждая се завершающая часть, начинающаяся с к -го шага (& = 1, N - 1), является оптимальной для остающихся шагов процесса. Другими словами, на каждом этапе решения, учитывая развитие всего процесса, оптимизируют только один шаг. И таким образом, при принятии решения учитывают будущее. Однако в каждом процессе есть последний к -й шаг, который нс зависит от будущего. Поэтому на этом шаге управление позволяет получить максимальный эффект. Спланировав к -й шаг, к нему присоединяют (к - 1), затем (к - 2) и т. д. Процесс динамического программирования как бы разворачивается от конца к началу.
Чтобы спланировать к -й шаг, надо знать состояние системы на (/: - 1) шаге. Если состояние на (к - 1) шаге неизвестно, то делают различные предположения о возможных состояниях системы на этом шаге. Для каждого предположения выбирают оптимальное управление на последнем к -м шаге. Такое оптимальное управление называют условно оптимальным.
Рассмотрим ^-шаговый процесс (рис. 4.6). Сделаем ряд предположений о возможных состояниях процесса на (к - 1) шаге. Обозначим эти состояния S k _i , S k _ ] 2 ,..., S k ^ r . На последнем найдем для каждого из этих состояний условно оптимальное управление и к, (x t _,), и к 2 (х А._,),..., и к г (х 4 _, г).
Таким образом, к -й шаг спланирован. Действительно, какое бы состояние система ни принимала на (к - 1) шаге, уже известно как следует поступить на &-м.
Аналогично поступаем на (к - 1) шаге, только условно оптимальные управления необходимо выбирать, учитывая уже выбранные условно-оптимальные на к -м шаге. В итоге, выполнив все переходы, получим координату х°.
Для первого шага предположений не делаем, т. к. значение х° задано, далее находим оптимальные управления, учитывая все уже найденные. Проходя от х°к х*, получаем искомое оптимальное управление для всего процесса. Используя принцип оптимальности, найдем необходимые условия, которым должна удовлетворять оптимально управляемая последовательность и,..., м v _,.

Рис. 4.6.
Рассмотрим конечный участок траектории - интервал
.
И допустим, что для интервалов найдены оптимальные управления и оптимальная траектория, включая
х к.
Остается найти управление н А,...,м у на конечном участке. Из принципа оптимальности следует, что {w A ,...,w v } определяется только состоянием
х к _ {
и целью поиска экстремума, которая для [
к
,
N]
имеет вид

при
х-х ч, й = и ч
целевая функция
Z k
имеет оптимальное значение (максимум или минимум). Обозначим
![]() его
его
Аналогично
Из принципа оптимальности можно записать следующие рекуррентные выражения:

Соотношения (4.19)-(4.20) позволяют последовательно найти функции Веллмана.
В„ (х Л -|), B N _ { {x N - 2),..., 5, (х°) - уравнения Веллмана.
Находя В к (х к ~"), к = N, N -мы одновременно находим управления ы,*(дг*’ 1), которые называются условно-оптимальными управлениями, а процесс их нахождения - условной оптимизацией.
Управление м.*(х*~"), найденное из уравнения (4.20), удовлетворяет принципу оптимальности: т. е. в зависимости от начального состояния х к ~" управления и к учитывает оптимизацию не только к-го шага, но и следующих за ним (N - к) шагов.
Итак, в результате условной оптимизации находят В к (х к ~") и и к (х к ~"), к = N, N- 1,..., 1. Теперь можно осуществить безусловную оптимизацию задачи (4.18), т. е. найти искомые оптимальные управления и = (ии ?) и оптимальную фазовую траекторию х = (х,°,..., х? ).
Т. к. значение B t (x°) равно оптимальному значению целевой функции всех N шагов, то
если х 0 - первая точка траектории, то х,° = х°.

Алгоритм метода динамического программирования
Этан I. Условная оптимизация.
Шаг 1. Находим условно-оптимальные управления г/*(х ЛЧ) и функцию Веллмана B N (x N ~") в соответствии с соотношением (4.19).
Шаг 2. Находим ^"""(х* -2) и /? v _,(x v ~ 2).
Шаг N. Находим м"(х°)и 5,(х°).
Этап II. Безусловная оптимизация.
Шаг 0. Находим х.° в соответствии с (4.21).
Шаг 1. Находим и 1 . и х по формулам (4.22).
Шаг N. Находим w. v и x. v .
Итак, метод динамического программирования даст эффективный алгоритм оптимизации решений. Алгоритм основан на решении рекуррентных уравнений Веллмана. При этом однократное решение сложной задачи заменяется многократным решением более простой. Все же процедура динамического программирования слишком громоздка, т. к. на каждом шаге решения необходимо запоминать В к (х*_,), и* (х*_,).
И хотя метод динамического программирования существенно упрощает исходные задачи, однако непосредственное его применение, как правило, сопряжено с громоздкими вычислениями. Для преодоления этих трудностей существуют приближённые методы динамического программирования.

Этап I. Условная оптимизация.
Найдем уравнения Веллмана по формуле (4.19).
Шаг 1. Я,(х 2) = шах
Диапазон и 3 найден из следующих соображений: так как
![]()
![]()
Учитывая, что х г е, получаем диапазон изменения м 3:
![]()
Функция - при всех значениях х является возрастающей аргу-
мента и поэтому ее максимум

Шаг 2. С учетом формулы (4.20)

Находим стационарную точку из условия -^-:
ШагЗ. B,(x°)= max (2 , -1 + -).